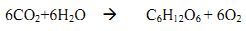CES Technical Report 131,   August 2013

¦ Home Page ¦ Content ¦ Publications ¦ Citation ¦ Contact ¦ PDF ¦  HOME  ¦

Section 1

Section 2

Section 3

Section 4

Section 5

Section 6

Section 7

Section 8

Section 9

Section 10

Above ground biomass and biomass productivity of three micro watersheds across altitudinal gradients in Western Himalaya

BACK  «  HOME  »  NEXT

Introduction

Bioresources
Bioresources are the resources we derive from living things around, bioresources play an important role in our system, as our dependency for food, fodder, energy etc.,
Bioresource in an ecosystem has two broad components, standing crop (living biomass) and litter. The former is the amount present in living components of the vegetation whereas the latter is an estimate of the dead plant parts which subsequently undergo the decomposition process. The primary step in the build up of biomass is photosynthesis. In this process, sunlight is absorbed by chlorophyll in the chloroplasts of green plant cells and is utilized by the plant to produce carbohydrates from water and carbon dioxide (Johansson et al. 1993). The process can be represented by the following equation.

                      sunlight

Biomass residues are the organic by-products of food, fibre and forest production. The most significant potential sources of biofuels are residues, wood resources from natural forests and biomass from managed plantations. Animal wastes like dung, skin, meat, bones and horns are well used in production of manure for agriculture. These animal residues can also be used as significant bioresources.

Of the different renewable energy sources, biomass appears to be the most important in terms of technical and economic feasibility during the next few decades in developing countries (Hall and Scrase, 1998). Regional policymakers, particularly those who consider options for meeting the energy needs at regional level require accurate assessment of bioresources. Biomass in all its form provides about 14% of the world’s energy (Hall et al.,1992). The annual per capita biomass energy consumption in developing countries is in range of 0.4 to 2 tonnes of wood. Most of the energy needs in India is met by biomass and bioenergy. The dependency on forest resources is high in developing countries like India, which has an estimated 328.73 Mha area that be used for biomass production under various classes like cropland, forests, plantation etc. (Bhattacharya et al., 2003). The projected biomass demand for India is around 516 Mt/yr. There is a clear need to develop indigenous energy sources, especially biomass resources in the developing countries, because of the growing rural energy problems. With the depletion of the non renewable energy there is an increase in demand for finding new ways to use renewable energy resources. The degree of dependence of rural communities on forests for their biomass needs varies depending on the degree and proximity of the forests (Ravindranath et al., 1991).

Energy from biomass has significant potential for more efficient production in the short term and for long-term inter fuel substitution. The biomass productivity is more in tropical forests than in the temperate region (Whittaker, 1975), but most of the tropical countries are developing nations and do require Bioresources to meet its needs especially in the rural area. This potential is particularly great in lower income developing countries with highly productive ecosystems.

Biomass
Biomass is defined as the total amount of aboveground living organic matter in trees expressed as oven-dry tons per unit area. The biomass is expressed in terms of weight per unit area, grams/square centimetre in case for microbes to tonnes/ha in case of forest or plantation biomass. Biomass estimation of vegetation in general, forests in particular has received serious attention over the last few decades for the very reason that components of climate change are associated with change in the biomass of a region. From ecosystem perspectives, biomass estimation helps in ecosystem productivity, energy and nutrient flows, and for assessing the contribution of changes in forest lands to the global carbon cycle. The potential carbon emission that could be released to the atmosphere due to degradation of forest and forest resource, deforestation and conversion of forested area into other land-use can be determined by biomass estimation. Hence, the precise estimation of biomass becomes necessary for understanding the importance of forest at regional scale.

Biomass can be categorised broadly as woody, non-woody and animal residues. Woody biomass comprises forests, agro-industrial plantations, bush trees, urban trees and farm trees. Wood, bark, branches and leaves constitute the above ground woody biomass. Woody biomass is generally a high valued commodity and has diverse uses such as timber, raw material for pulp and paper, pencil and matchstick industries, and cooking fuel. Woody biomass is derived from sources like forests, plantations and from wastelands.
Non-woody biomass comprises crop residues like straw, leaves and plant stems (agro-wastes), processing residues like saw dust, bagasse, nutshells and husks, and domestic wastes (food, sewage, etc.). They are harvested at the village level and are essentially used either as fodder or cooking fuel and animal residues constitutes the waste from animal husbandry These traditional fuels are especially important in developing countries, where they meet a large portion, of energy needs (Ramachandra et al., 2004).

The actual energy content measured as the heating values is an important characteristic of biomass when it is considered as an energy source. It measures the quality of fuel in combustion applications. For woody biomass resources, the moisture content of the wood impedes the available energy, while for non-woody biomass, the ash content and the moisture content affect its energy values.

Forest Biomass
Forests play an important role in global carbon cycling, since they are large pools of carbon as well as potential carbon sinks and sources to the atmosphere. Accurate estimation of forest biomass is required for greenhouse gas inventories and terrestrial carbon accounting. The needs for reporting carbon stocks and stock changes for the Kyoto Protocol have placed additional demands for accurate surveying methods that are verifiable, specific in time and space, and that cover large areas at acceptable cost ( Krankina et al. 2004; Patenaude et al. 2005; UNFCCC, 1997).

Biomass production and accumulation integrate plant responses to biotic and abiotic features of their environment. Forest biomass varies over climatic zone, altitude and region (Brown et al., 1989). Plant biomass is therefore a metric fundamental to understanding and managing forest ecosystems, whether to estimate primary production, nutrient pools, species dominance, responses to experimental manipulation, or fuel loads for fire. In recognition of its central importance, models of ecosystem processes often include plant biomass or biomass-related variables as inputs and outputs (Northup et al. 2005). Forest biomass is important for both commercial (timber, non-timber forest produce, etc.) and non-commercial (e.g., fuel wood assessment) uses. This is useful in national development planning, as well as in scientific uses such as studies of ecosystem productivity, energy and nutrient flows, and for assessing the contribution of changes in tropical forest lands to the global carbon cycle. Hence, estimating forest biomass helps in assessing fuel wood stock, carbon stock (Lugo, 1982; Brown et al., 1989), and are equally important in estimation of forest productivity and carbon fluxes, assessing sequestration of carbon in wood, leaves and roots (Cole and Ewel, 2006), etc. 

Characterizing the composition, structure and function of ecosystems is done through the assessment of the above ground biomass (AGB), which is of value not only for theoretical understanding of energy and element flows within the ecosystem, but also from a more practical point of view, as an indicator of ecological impacts.

Evaluation of the patterns, processes and dynamics of C cycling in forest ecosystems at local, regional and global scales (Luo et al., 2002) are done through the assessment of Net primary productivity (NPP) and biomass productivity. Net primary production is the difference between total photosynthesis (Gross Primary Production, GPP) and total plant respiration in an ecosystem. Alternatively, NPP is defined as the total new organic matter produced during a specified interval. NPP is usually defined as the balance between the light energy fixed through photosynthesis and lost through respiration and mortality, representing the net C uptake from the atmosphere into vegetation. Biomass productivity indicates the amount of biomass (leaf litter, dead wood, twigs, etc) available on renewable basis, which depends on the species, type of ecosystem, etc.

Plantations
Biomass from plantations has been recognised as a viable alternative to conventional energy resources. The establishment of forest plantations for the production of biomass, to be used as an energy source has attracted considerable interest since the late 1970’s. The productivity of these plantations depends on different factors such as species, soil quality, rainfall, silvicultural practice, planting space, etc., and varies from 0.8 to 6.0 t/ha/yr for tropical countries. In India, faster growing tree species like poplar, Eucalyptus, Acacia, etc., are preferred in social forestry or adhoc afforestation programmes wherein a quicker yield is given over a short period of time. However, biomass production from plantations, have varying results.

In case of India, the productivity of Eucalyptus species for barren uncultivable land is estimated to be 3 t/ha/yr (air dry) due to degraded land condition. A productivity of 6.6 t/ha/yr has been assumed as the productivity for short rotation plantation on other land categories. The productivity of plantations with genetic improvement of seeds is assumed to be 8 t/ha/yr and the addition of fertilisers is assumed to enhance the productivity to 12 t/ha/y (Bhattacharya et al., 2003). Above ground biomass (standing biomass) in plantations of Himalayan region has given an estimate of 273 t/ha for an age of 25 years. Standing biomass in a central Indian plantation of monoculture Gmelina arborea is estimated as 3.6 t/ha for one year old plot to 56.4 t/ha for 6 year old plot (Swamy et al., 2004).

Karmacharya and Singh (1992) estimated the productivity and biomass of a teak plantation in India, they developed a regression equation of type log Y= a+ b log X, where Y is biomass component of the tree (kg) and X is the girth at breast height (GBH in cm). The predicted and the initial estimates were strongly correlated (r=0.99, df= 32, P< 0.001 ). Total aboveground biomass increased from 25 t/ha at 4 years to 77 t /ha at 30 years. Teak trees showed measurable and varying annual girth increments. Mean annual increment varied with girth class, being maximum (6.7 cm/yr) in the 15-20 cm girth class and minimum (1.7 cm/yr) in the greater than 70 cm girth class.

Agriculture
Biomass from agriculture is very significant; tonnes of agricultural residues are produced each year after the harvest season. Earlier these residues were used to make agricultural manure, but with advanced technology, biogas and electricity are being produced.

Biomass in Himalaya

In the Himalaya, vegetation ranges from tropical monsoon forest to alpine meadow and scrub, across elevation gradients. The Himalayan forest biomass is important as a large population of hill folk are still dependent on forest biomass to meet their daily requirement (Singh and Singh, 1991). The trend in biomass in the Himalayan region shows an increase in biomass with increase in altitude for different strands up to an altitude of 2700 m and shows decrease hence on, as the vegetation above 3000 m is sparse and are mostly of alpine grassland types at above 3500 m (Singh et al., 1994). Pinus roxburghii Sarg. (chir pine) forest are dominant along the low-to-mid montane belt of Central and Western Himalaya (Chaturvedi and Singh, 1987) with high regeneration potential, growth rate, establishing in degraded habitats, pipe like boles and high volumes. A sustained regeneration and growth in the presence of older plants is required for better growth of any plant community (Ramakrishnan et al., 1981).

Knowledge on ecological processes and biotic pressure helps in understanding the persistence of long-lived plant communities, as disturbance is widespread all over the Himalaya (Singh and Singh, 1991). Humans have made considerable impacts in the Himalayan region, estimating such changes accurately would be of particular value to Himalayan people, whose subsistence agriculture depends on forest productivity to maintain livestock and soil fertility.

Factors Influencing Biomass
Forest degradation and/or fragmentation have significant impacts on the biomass of forest stand. Recent concerns about global warming and the carbon sequestration potential of tropical rainforests highlight the importance of regenerated secondary forests and their role as a carbon sink. Fire can also have a high toll on the biomass of forests. In the humid tropics, if fire kills large primary tree species, the burned area becomes dominated by a few pioneer tree species and the lost biomass is unlikely to be completely restored. In addition, degraded lands without parent trees may not have the potential for succession leading to replacement. Therefore, biomass recovery in such areas is quite slow and there may be limits to the potential above ground biomass.

In India, large areas of primary tropical forests are either degraded to different degrees or converted to other uses, like agriculture, urban and industrial development. Major causes of this degradation are habitat destruction, over exploitation, pollution and species introduction. Forest destruction is considered as one of the most serious environmental and economic problems for many countries in the tropical and sub-tropical regions of the world (Sharma, 1996). In India, 72% of existing forest has lost the capacity for regeneration. However, tropical forests have high regenerating capacity and if protection measures are extended they can recover very well (Behera et al., 2006). Lopping intensity has proven to have impact on biomass of forests, leading to reduction in growth of tree girth and production of leafy biomass (Bhat et al., 1995).

Biomass Estimation
The total inventory is divided into land and water. Land is divided into forest and non forest, and forest into productive and unproductive. For an assessment of forest biomass, forest inventory is most commonly used and it differs depending on scope and purpose. Inventories are being designed to obtain information on other uses of the forest like recreation, grazing, wildlife and water conservation. It is designed to measure forest biomass rather than or in addition to traditional volume. Species specific equations that describe relationships between plant attributes and biomass are more accurate and flexible. Furthermore, it is preferable to use region or site-specific relationships where possible. Species size–biomass relationships could differ as plants alter allocation patterns in response to soil, climate and disturbance. Changes in structure and composition of vegetation are often accompanied by changes in biomass.

Destructive Methods
Forest biomass varies over climatic zone, altitude and region (Brown et al., 1989; 1991) and there is no standard method to estimate biomass. Different methods are used for different study region. The methods that have been developed so far include the destructive and non-destructive sampling and most are based on harvested methods (Utsov et al., 1997). The destructive sampling involves harvesting reasonable samples and estimating wood density and AGB. The next stage involves deriving the probable relationship between the parameters viz., tree girth, height with AGB. Destructive sampling provides reasonably accurate yield, but cannot be carried in all situations, hence biomass estimation through indirect method from basal area, height, etc is adapted nowadays.

Non-destructive Methods
In non-destructive techniques, forest biomass is estimated mathematically, using functions (based on earlier experiments involving parameters such as tree girth, height, etc), which relate the diameter of a tree to its biomass- or parts of its biomass- (leaves, bark, bole wood etc). Much work has been done to make the necessary measures and calculations to prepare these functions for many species (Jenkins et al., 2004). Brown et al., (1997) arrived at a non-destructive sampling strategy through the biomass estimation methods for the forests of the tropical region, based on regression models that were derived from known samples, which were cut and measured. Advances in the field of remote sensing and GIS, has given further boost to these techniques in estimating forest biomass over large region.

A protocol for forest biomass assessment based on the allometric equations will involve four steps (Ketterings et al., 2000):

1. choosing a suitable functional form for the allometric equation;
2. choosing suitable values for any adjustable parameters in the equation;
3. field measurements of the input variables such as tree diameter (DBH), height, etc., and
4. using the allometric equation to give the above ground biomass of individual tree and summation to get area estimates.

A detailed summary of biomass density studies in tropical forests, from lowland to montane and from wet to very dry zones, was made by Brown and Lugo (1982). Olson et al., (1983), produced a global map of the biomass density of all ecosystem types, including disturbed and undisturbed forests at a 0.5° x 0.5° grid-scale of resolution.

AGB as given in equation 1, is computed considering VOB (volume of biomass)/ha and accounting for volume-weighted average wood density and biomass expansion factor (Brown and Lugo 1992). Above ground biomass is given by:

AGB(t/ha) = VOB * WD * BEF        ..........................................................................Equation 1

where WD = volume-weighted average wood density (1 ton of oven-dry biomass per m3 green volume) and BEF = biomass expansion factor (ratio of aboveground oven-dry biomass of trees to oven-dry biomass of inventoried volume).

Wood density is expressed in units of mass of wood per unit of volume (either tons/m3 or grams/cm3) at 12% moisture content. Reyes et al., (1992) derived the relationship between wood density with 12% moisture content to wood density based on oven-dry mass per green volume and is given by Y = 0.0134 + 0.800X (r2= 0.99; number of data points n = 379), where Y is wood density based on oven-dry mass/green volume and X is wood density based on 12% moisture content. The term BEF is defined as the ratio of total aboveground oven-dry biomass density of trees with diameter at breast height (DBH) ≥10cm to the oven-dry biomass density of the inventoried volume and is given by BEF = Exp{3.213 - 0.506*Ln(BV)} for BV < 190 t/ha (sample size = 56, adjusted r2 = 0.76) or BEF=1.74 for BV>=190t/ha where BV is biomass of inventoried volume in t/ha, calculated as the product of VOB/ha (m3/ha) and wood density (t/m3).

Another approach for AGB estimation is by regression models considering varioius components like tree top, foliage, branches, bole, stump and root using known samples. One desirable attribute of tree biomass equation is that they be additive, i.e., the sum of the biomass of components is equal to the total tree biomass for a given species.

The tree biomass equations are similar to tree volume equations relating volume and biomass with variables like height (H) and Diameter at Breast Height (DBH).

V= a +b D²H   ....................................................................................................................Equation 2                      
B= a + bD²H   ....................................................................................................................Equation 3

V is volume , B is biomass (Kg  ), D is DBH ( cm  )and H is height of tree ( metre ).

There are also other regression models relating biomass with variables using log values (Brown et al., 1997) as listed below
.
Y=exp{a+b*ln(D)}.............................................................................................................Equation 4
Y=10^{-a+log₁₀ (BA)}.......................................................................................................Equation 5
Y=a+b(D)+c(D²).................................................................................................................Equation 6
Y=exp{a+b*ln(D)}.............................................................................................................Equation 7

Remote Sensing and GIS Techniques

Remote sensing is the art of acquiring information from an object without coming in actual contact with it. Many methods have been developed to estimate and map forest biomass from remotely sensed data (Foddy et al., 2001). Satellite remote sensing is the only way to acquire synoptic views over the huge expanses of inaccessible tropical forests. Forested land covers in the tropics are being differentiated using satellite digital and photographic data. Also, it can be used to differentiate secondary forests from primary forests and non-forested areas in the tropics.

Vegetation indices have, in particular, been used widely in land-cover analysis. A vegetation index expresses the remotely sensed response observed in two or more wavebands as a single value that is related to the biophysical variable of interest (Mather, 1999). An index may be easily applied to the imagery and thereby produce a representation of the spatial distribution of the biophysical variable of interest. Numerous indices have been proposed (Mather, 1999) but the most popular is the NDVI (Normalised difference vegetation index), which is given by:

NDVI = (IR - R)/(IR + R),

where, IR and R represent the near-infrared and red wavebands, respectively. There are, however, problems with the use of vegetation indices such as the NDVI. First, the relationship between the vegetation index and biomass is asymptotic and this can limit the ability of the index to represent accurately vegetation with a large biomass (Ripple, 1985). Secondly, it is essential that the remotely sensed data be accurately calibrated, typically to radiance, if the calculated index values are to be correctly interpreted and compared (Mather, 1999). Thirdly, the sensitivity of vegetation indices to biomass has been found to vary between environments (Ringrose et al.,1994). Fourthly, most vegetation indices fail to use all the spectral data available. Typically, a vegetation index uses only the data acquired in two spectral wavebands, yet the sensor typically acquires the spectral response in several additional wavebands.

Massanda et al., (2003) gave a method to estimate biomass using remote sensing, aerial photography and allometric equations. Photogrammetric methods were used in order to measure tree height and tree crown diameter, using aerial photographs. The measurements were then transformed to biomass, using an allometric equation generated through trees that were cut and oven dried and weighed. Luther et al., (2006) developed a model called BIOCLUST to estimate biomass from forest type and structure using Landsat TM imagery. This technique is useful in estimating and mapping biomass of large areas with maximum accuracy.

Biomass in Tropical Region

Regression models were developed by researchers in the tropical region (Brown et al. 1997), for estimating above ground biomass through non destructive measures and measures from forest inventories. The biomass regression equations can provide estimates of biomass per tree. The equation developed were regardless of species and was done zone wise: dry zone where rainfall is considerably less than potential evapotranspiration (e.g. <1500 mm rain/year and a dry season of several months), moist or where rainfall approximately balances potential evapotranspiration (e.g. 1500-4000 mm rain/year and a short dry season to no dry season), and wet or where rainfall is in excess of potential evapotranspiration (e.g. >4000 mm rain/year and no dry season). Probable relationship between AGB and Girth of trees were derived based on field samples in various climatic zones are listed in Table 1.

Table 1. Regression models for estimating AGB in various climatic zones.

The drawbacks associated with this technique are – a) use of trees of various girth classes, b) wide and often uneven-width diameter classes, c) multiple branching and buttresses and selection of the appropriate average diameter to represent a diameter class, and d) missing smaller diameter classes.  To overcome the potential problem of the lack of large trees, equations were selected that were expected to behave reasonably up to 150 cm or so or upon extrapolation somewhat beyond this limit (Brown et al. 1989).

Murali et al., (2000) compiled equations for estimating biomass in tropical forest, which are listed in Table 2.

Table 2. List of AGB (Y in t/ha) equations for tropical forest.

Parameters	Linear	Log
Deciduous (n=11)	Y=-73.55+10.73(basal area) (r2=0.82; % error =48)	Y=-1168.66+429.63*ln(basal area) (r2= 0.87; % error = 24.98)
Evergreen (n=84)	Y=-2.81+6.78(basal area) (r2=0.53; %error =74)	Y=3.51+0.036*ln(basal area) (r2=0.28; % error=79.5)
Deciduous (n=10)	Y=11.27+6.03(basal area)+1.83(height) (r2=0.94; % error = 49)	Y=-766+452.19*ln(basal area)-166.66*ln(height) (r2=0.94; %error=28.94)
Evergreen (n=52)	Y=34.97+10.98(basal area)-6.77(height) (r2=0.94; % error= 80)	Y=-961.65+276.85*ln(basal area)+86.32*ln(height) (r2=0.53; % error = 88.89)
Deciduous (n=10)	Y=-160.64-0.025(density)+15.4(basal area) (r2=0.92; % error=27.8)	Y=-957.1-44.07*ln(density)+460.63*ln(basal area) (r2=0.91; % error=31)
Evergreen (n=52)	Y=120.67-0.01(density)+5.73(basal area) (r2=0.6; %error 60.6)	Y=-142.24-47.65*ln(density)+230.54*ln(basal area) (r2=0.57; % error=26.4)
Deciduous (n=10)	Y=227.2+0.03(density)-3.54(height) (r2=0.46; % error = 123)	Y=-439.2+40.3*ln(density)-134.17*ln(height) (r2=0.14; % error =12.9)
Evergreen (n=40)	Y=5.74-0.14(density)+0.312(height) (r2=0.6; % error=88.26)	Y=-142.24-47.65*ln(density)+230.63*ln(height) (r2=0.49;% error =98)
Deciduous (n=10)	Y=-56.8-0.015(basal area)+13.6(height)-4.21(density) (r2=0.92; %error =27.8)	Y=-760.94-6.4*(basal area)+455.05*ln(height)-155.82*ln(density) (r2=0.94;% error = 26.62)
Evergreen (n=39)	Y=123.26-0.008(basal area)+5.63(height)-0.27(density) (r2=0.62; % error=86.79)	Y=-631.98-32.75*(basal area)+288.87*ln(height)+52.20*ln(density) (r2=0.59; % error=95.16)

Path coefficient analysis based on parameters of the above equations showed that only basal area has significant correlation with biomass, compared to height and density. Deciduous forests had higher correlation between biomass and basal area.

Biomass estimate throughout the tropical region varied from 30–900 t/ha based on species composition, age and level of degradation in forest. Behera and Mishra (2006) noted the variation in AGB over age of strand in recovering tropical sal (Shorea robusta) forests of Eastern Ghats of India. Table 3 lists regression models and estimated AGB based on the same.

Table 3. Regression models and estimated AGB for tropical forests

Chave et al. (2005, equation 14), derived a biomass estimation equation for tropical dry forests, which draws upon data from 404 trees from India, Australia and Mexico (refer table 3). Mani and parthasarathy (2006, equation 16, 17) developed regression equation for inland and coastal tropical dry evergreen forests of peninsular India. The above ground biomass varied from 39.69 to 170.02 t/ha and by inclusion of height (in m), it varied from 73.06 to 173.10 t/ha. Aboal et al., (2004, equation 13), derived the allometric relationship based on samples of different tree species and stand above ground biomass in an island, and the estimated AGB varied from 65 to 352 t/ha. Haripriya (2000) reported the above ground biomass of Indian forests to be in range of 14 to 210 t/ha, with a mean of 67.4 t/ha. According to this study, most of the biomass is concentrated in lower diameter classes of potentially large species, thus making it potential to sequester carbon over a long period of time. Nascimento and Laurence (2001, equation 18), estimated AGB of Amazon forests as 397 t/ha ±30 t/ha. A significant result in this study was biomass varied widely within the large study region, hence biomass estimation should be extensive. Tropical forest biomass based on published literatures (listed in Table 4) shows that the AGB ranges from 78.1 – 689.7 t/ha (Brown and Lugo, 1992) and for Indian region it ranges between 14-210 t/ha (Haripriya, 2004).

Table 4. Estimated AGB for various Tropical forests.

Biomass in Temperate Region

Johnson and Risser (1974) estimated AGB of temperate oak forest, based on Whittaker et al., (1967). The biomass obtained was 245 t/ha, which is comparable to the estimate of 100 to 500 t/ha for a broad range of temperate deciduous forests. Whittaker (1975) gave estimated values for fir forests in temperate region to be around 360-440 t/ha, and for pine forest in range of 130-210 t/ha (equations 20, 21). Wang (2005) developed allometric equations (#19) for ten co-occurring species based on destructive sampling of temperate region in China. Humus layer biomass ranged from 67.0 to 153 t/ha at different sites in the temperate forest. AGB estimates for temperate forest are listed in Table 5.

Table 5. AGB equations for temperate regions based on forest types or stands.

Luo et al., (1996) have derived regression equations for China and Tibet plateau comprising temperate forests and are listed in Table 6. The AGB estimate varies from 14-727 t/ha for various forest types with the maximum value for evergreen broad leaved forest type. The regression equations were calculated for individual species of the temperate region, as well for a forest type or stand, which are listed in Table 6.

Table 6. AGB equations for individual species of the temperate region

Species	Equation	Equation #	Ref
Cupressus torulosa	AGB=-2.8232+.9268D	22	Luo et al., 2002
Ficus nemoralis	AGB=7.5*10-2*(D) 2.6	23	Hiratsuka et al., 2006
Lyonia ovalifolia	lnAGB=-2.155+2.356*lnD	24	Mohns et al., 1988
Myrica esculenta	AGB=-2.286+2.496D	25	Mohns et al., 1988
Pinus roxburghii	AGB=23.9124+.5232D	26	Luo et al., 2002
Pinus roxburghii	AGB=-5.106+3.022D	27	Mohns et al., 1988
Pinus roxburghii	AGB=-6.398+2.655D	28	Chaturvedi and Singh, 1987
Pyrus pashia	lnAGB=.043+2.072lnD	29	Mohns et al., 1988
Quercus glauca	AGB=1.8409D0.89262	30	Luo et al., 2002
Rhododendron arboreum	lnAGB=-1.628+2.24lnD	31	Mohns et al., 1988
Quarcus species	AGB=0.113+2.4572D	32	www.classes.yale.edu
Acer sp.	AGB=.01008+2.5735D	33	www.classes.yale.edu
Vitis	AGB=.0617+2.5328D	34	www.classes.yale.edu

Biomass in Himalayan forest

Garkoti and Singh (1995), studied the variation in biomass and productivity in a central Himalayan forest region through an altitudinal gradient using 10m X 10m quadrat in each strata. Singh and Singh (1991), developed allometric equation for different parts of the tree, in addition to interspecies allometric equation for non-dominant tree species. Rana et al., (1989) estimated AGB in an altitudinal gradient of 300-2200m in the central Himalayas as 199 to 787 t/ha. The representative forest communities are sal (Shorea robusta Gaertn. F.) between 300 and 900 m; chir pine (Pinus roxburghii)/mixed-broadleaf forest from 900 to 1200 m; chir-pine forest from 1200 to 1800 m; mixed banj-oak (Quercus leucotrichophora)/chir-pine forest from 1500 to 2000 m; and mixed-oak (Quercus sp.) forests between 1800 and 2500 m (Table 7).

Table 7. Estimated AGB for various Himalayan region.

The biomass distribution in trees were in the range of 40 to 60% in the bole, and is found to be low in oak forest than others, this is comparable to Negi et al., (1983). The allocation of biomass to branches was greater (40-45.2%) in oak-dominated forest compared with the other forests as dominance of leader shoot over the laterals was less marked in oaks than in the others. The contribution of foliage to the above-ground biomass was 3.4-5.1%, which falls in the range 2.6-9.3% reported for certain temperate and tropical forests of the world (Johnson and Risser, 1974; Whittaker, 1975; Singh, 1979; Negi et al., 1983; Rawat, 1988).

The range of forest biomass (199-787 t/ha) in the Central Himalaya (up to 2200-m elevation) was comparable to the range of biomass (200-600 t/ha ) generally found in the mature forests of the world (Whittaker, 1975). The tree biomass in chir-pine forest and chir-pine/mixed-broadleaf forest (respectively, 199 t/ha and 192 t/ha ) was similar to that of a 38-year-old chir-pine forest of this region studied by Chaturvedi and Singh (1982).

The biomass of various strand within a temperate watershed in Sikkim region varied from 368 to 682 t/ha with a mean of 596 t/ha (Sundriyal and Sharma, 1996). Negi and Tadoria (1993) estimated the biomass consumption as 442 kg/person/year in rural Garhwal Himalayas. Such high dependency on forest biomass has led to considerable degradation in the forests of the Himalayan region. Singh et al., (1994) compiled the biomass estimation in different Himalayan region, which are listed in Table 8.

Table 8. Species wise AGB and Net Productivity in Himalayan forests.

Forest type	Elevation (m)	Density (#/ha)	Basal area (sq.m/ha)	Biomass (t/ha)	Net productivity (t/ha/yr)
Shorea robusta	300	443	56.4	710	15.5
Shorea robusta	350	726	41	455	18.8
Pinus roxburghii	1300	700	45.4	29	18.7
Pinus roxburghii	1400	820	40.2	208	17
Pinus roxburghii	1600	1630	25	113	7.6
Pinus roxburghii	1700	540	47.2	283	16
Pinus roxburghii	1750	657	37	199	17.3
Mixed oak	1850	783	40	426	15.9
Quercus leucotrichophora	1950	570	36.8	388	13.2
Quercus lanata	2150	993	60	557	17.8
Quercus lanata	2190	660	35.8	285	15.5
Quercus floribunda	2190	760	33.9	459	16.6
Quercus floribunda	2200	1107	71	782	25.1
Mixed oak	2200	598	55	344	15
Cedrus deodara	2200			451	28.2
Aesculus indica	2300	280	59.7	502	16.5
Abies pindrow	2500	350	105.6	565	17.8
Quercus semecarpifolia	2650	480	73	590	19.5
Acer cappadocicum	2750	505	35.8	305	14.5
Betula utilis	3150	700	23.2	172	12.5
Rhododendron campanulatum	3300	1180	14.9	40	7.5

The above result shows that there is a decrease in biomass after an elevation of 2400m and more abruptly after 3300m. Tree density and basal area varied in the middle altitude. Lower elevation (<1500m) strands had less mean basal area.  Stands above 3000m were composed of trees of coniferous type having high basal area but low density. The lower elevation is composed of low to moderate number of small trees, while mid elevation stands varies in tree size and density both within and among forest types, largely due to the stands of Quercus sp.

The relationship of tree density and total basal area varied widely, within and among forest types. In the central Indian Himalayas (foothills to 2600m elevation), AGB varied from 500-600 t/ha. However, much lower biomass estimates of 200 t/ha occurred in early successional P. roxburghii between 1300 and 1750 m elevation. Above 2600 m, biomass declined sharply to 170 t/ha in birch forest with rhododendrons, at 3100-3200 m elevation. At  3300m elevation in pure thickets of small-stature rhododendrons, the biomass was 40 t/ha. In two stands, one of S. robusta forest at 300m and the other in Q. floribunda forest at 2200m elevation, forest biomass exceeded 700 t/ha. These two stands appeared to represent a limit for biomass values for elevations below 2200m. Biomass values up to 2400 t/ha occurred up to 3400 m elevation in the Nepal central Himalaya forests of a given biomass occurred several hundred metres higher in Nepal than in Kumaun. In both Kumaun and Nepal, Q. semecarpifolia forest attained similar maximal biomass, up to 550-600 t/ha near 2600 m elevation.

Productivity

Net primary productivity (NPP) and above ground biomass (AGB) are two widely used indices in evaluation of the patterns, processes and dynamics of Carbon cycling in forest ecosystems at local, regional and global scales (Luo et al., 2002).

Net primary production is the difference between total photosynthesis (Gross Primary Production, GPP) and total plant respiration in an ecosystem. Alternatively, NPP is defined as the total new organic matter produced during a specified interval. NPP is usually defined as the balance between the light energy fixed through photosynthesis (gross primary productivity) and lost through respiration and mortality, representing the net Carbon uptake from the atmosphere into vegetation (Mellino et al., 1993).

Equations involving the basal area are used for all tree species and therefore are used to estimate the standing biomass of mixed forests. Productivity, which is the increase in weight or volume of any biomass over a period of time, can be estimated when the standing biomass estimates are available for two consecutive years. It can also be calculated, by knowing the age of the forest stand in addition to the litter available annually. Productivity is equal to standing biomass per hectare/age of a tree or the trees per forest stand. Productivity estimates are important as they help to calculate the extent of biomass that can be extracted for fuel purposes (Ramachandra et al., 2004)

Another method used to find the productivity of a central Himalayan forest is by collecting the litter fall, where in litter fall is recorded on a monthly basis, by collecting the litter in a 50cm X 50cm X 15cm wooden trap with nylon mesh. The litter is sorted into leaf, wood and miscellaneous components. A sample plot of 1ha is marked, where the increase in GBH is measured annually. Dry biomass increments of different tree components can be calculated using the biomass equations. The annual biomass accumulation can be calculated from the net changes in biomass. The sum of accumulation for different tree components yielded the net biomass accretion for the trees. And the weight of litter collected in a defined area annually is added to the foliage biomass accumulation to calculate foliage production. Wood reproductive parts and miscellaneous litter fall values were summed in biomass accumulation of twigs to give the productivity for an interval (Garkoti and Singh, 1995).

Clarke et al., (2001) developed a conceptual method to calculate NPP (net primary productivity) with two approaches.

Approach 1:
Stand Increment = (Σ Increments of surviving trees) + (Σ  Increments(s) of ingrowth)

Approach 2:
Stand Increment = ( Σ AGB at t₂ - Σ AGB at t₁) + ( Σ Biomass of trees that died in the Interval) - [(Biomass of a minimum size tree) x (number of new trees)]

Rana et al., (1989) also estimated the net primary productivity in the Himalayan region, which was in the range of 12.8-27.9 t /ha/year and was not related to the elevation. Mohns et al., (1988) gave the productivity for pine forest to be 0.6-6.7 t/ha/yr. According to this study the Broad-leaved tree biomass ranged from 5.1-24.2 t/ha with productivity rates between 1.8 and 6.7 t/ha/year.

References

1. Aboal Jesus Ramon, Arevalo Jose Ramon, Fernandez Angel. 2005. Allometric relationships of different tree species and stand above ground biomass in the Gomera laurel forest  (Canary Islands), Flora, 200: 264–274
2. Behera S K., Misra M.K. 2006. Above ground biomass in a recovering tropical sal (Shorea robusta Gaertn.f.) forest of Eastern Ghats, India.  Biomass and Bioenergy, 30:509–521
3. Bhat D.M., Ravindranath N.H. 1995. Tropical forest biomass. Centre for Ecological Sciences, Indian Institute of Science, Technical report – 77.
4. Bhat D.M., Ravindranath N.H., Gadgil M., 1995. Effect of Lopping intensity on tree growth and stand productivity in tropical forest. Journal of Tropical Forest Science, 8: 15-23
5. Bhatt, B. P., Sachan, M. S. 2004. Firewood consumption along an altitudinal gradient in mountain villages of India, Biomass and Bioenergy, 27:69-75.
6. Bhattacharya, S. C., Salam, P. A., Pham, H. L., Ravindranath, N. H. 2003. Sustainable biomass production for energy in selected Asian countries, Biomass and Bioenergy, 25:471-482.
7. Brown S, Gillespie A. J. R., Lugo A. E. 1991. Biomass of tropical forests in South and Southeast Asia. Canadian Journal of Forest Research. 21: 11 1-117.
8. Brown S, Lugo A. E. 1982. Storage and production of organic matter in   tropical forests and their role in the global carbon cycle. Biotropica. 14: 161-187.
9. Brown S. 1989, Estimating Biomass and Biomass Change of Tropical Forests: a Primer.(FAO Forestry Paper - 134): http://www.fao.org/docrep/W4095E/w4095e00.HTM
10. Brown Sandra, Schroeder Paul, Birdsey Richard. 1997. Aboveground biomass distribution of US eastern hardwood forests and the use of large trees as an indicator of forest development, Forest Ecology and Management. 96:37-47.
11. Brown Sandra., Schroeder Paul, Kern Jeffrey S. 1999.  Spatial distribution of biomass in forests of the eastern USA, Forest Ecology and Management. 123: 81-90
12. Brown, S and A.E. Lugo, 1990. Tropical secondary forests, J. Trop. Ecol. 1990: 1–32.
13. Brown, S., 1997. Estimating biomass and biomass change of tropical forests. A primer. FAO Forestry Paper 134. Food and Agriculture Organization of the United Nations, Rome, Italy.
14. Chave J., Andalo C., Brown S., Cairns M. A., Chambers J. Q., Eamus D., Folster H., Fromard F., Higuchi N., Kira T., Lescure J.-P., Nelson B. W., Ogawa H., Puig H., Riera B., Yamakura T., 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests, Oecologia, DOI 10.1007.
15. Chave Jérôme, Condit Richard, Lao Suzanne, Caspersen John P., Foster Robin B. Hubbell Stephen P. 2003. Spatial and Temporal Variation of Biomass in a Tropical Forest: Results from a Large Census Plot in Panama, Journal of Ecology,  91:240-252.
16. Chaturvedi O.P and Singh J.S, 1987, The Structure and Function of Pine Forest in Central Himalaya. I. Dry Matter Dynamic, Annals of Botany 60: 237-252
17. Cole T.G., Ewel J.J. 2006. Allometric equations for four valuable tropical tree species. Forest ecology and management. 229:351-360. 1-9.
18. Foody Giles M; Mark E. Cutler; Julia McMorrow; Dieter Pelz; Hamzah Tangki; Doreen S. Boyd; Ian Douglas, 2001, Mapping the Biomass of Bornean Tropical Rain Forest from Remotely Sensed Data, Global Ecology and Biogeography, Vol. 10, No. 4 pp 379-387.
19. Garkoti S.C, Singh S.P, 1992. Variations in the Net primary productivity and Biomass of forests in high altitude region in the central Himalayan region. Journal of Vegetation Science, 1:23-28
20. Gillespie, A.J.R., Brown, S. and Lugo, A.E., 1992. Tropical forest biomass estimation from truncated stand tables. Forest Ecology and Management. 48: 69-87.
21. Hall R.J., Skakun R.S., Arsenault E.J., Case B.S., 2006. Modeling forest stand structure attributes using Landsat ETM+ data:Application to mapping of aboveground biomass and stand volume, Forest Ecology Management 225: 378-390
22. Hall, D. O. 1991. Biomass energy, Energy Policy, 19:711-737.
23. Hall D.O., F. Rosillo-Calle and P. de Groot, 1992, Lessons from case studies in developing countries , Biomass energy, Vol 1, pp 62-72
24. Hall, D. O.,Scrase, J. I. 1998. Will biomass be the environmentally friendly fuel of the future?, Biomass and Bioenergy, 15:357-367.
25. Hall, D.O., House, J.I.1994. Biomass energy development and carbon dioxide mitigation options. In: Proceeding of the International Conference: National Action to Mitigate Global Climate Change, Copenhagen, Denmark.
26. Haripriya, G. S. 2000. Estimates of biomass in Indian forests, Biomass and Bioenergy, 19:245-258.
27. Haripriya G.S 2004, How ‘sustainable’ is the ‘sustainable development objective’ of CDM in developing countries like India? Forest Policy and Economics-6, pp 329-343
28. Jensin C.Jennifer, David C.Chojnacky, Linda S. Heath, Richard A. birdsey, Comprehensive Database of Diameter-based Biomass Regressions for North American Tree Species, 1981, USGS Forest Services pp 1-48
29. Johnson FL, PG Risser, 1974, Biomass, Net primary productivity and synamics of six mineral elements in a Post Oak Black jack oak forest, Ecology, Vol 55 pp 1245-1258
30. Johansson T.B., Kelly, H., Reddy, A.K.N., Williams R.H. 1993. Renewable energy sources for fuels and electricity. Island Press, USA.
31. Karmacharya S.B, Singh K.P 1992. Biomass and net production in teak plantation in a dry tropical region in India. Forest Ecology and Management 55; 233-247
32. Ketterings Quirine M., Coe Richard, Noordwijk Meine van, Ambagau Yakub and Palm Cheryl A. 2001. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests , Forest Ecology and Management ,146:199-209.
33. Krankina Olga N, Mark E. Harmon, Warren B. Cohen ,Doug R. Oetter, Zyrina Olga and Maureen V. Duane, 2004, Carbon Stores, Sinks, and Sources in Forests of Northwestern Russia: Can We Reconcile Forest Inventories with Remote Sensing Results? Climate Change, Vol 67: No. 2-3, pp 257-272
34. Lal, J.B. Forest Biomass Estimation, Technical Report from Forest Survey of India,           Dehradun.
35. Luo tianxiang, Li wenhua, and Zhu huazhong. 2002. Estimated biomass and productivity of natural vegetation on the Tibetan plateau, Ecological Applications, 12:980–997
36. Luther, J., Fournier, R., Piercey, D., Guindon, L., Hall, R. 2006. Biomass mapping using forest type and structure derived from Landsat TM imagery, International Journal of Applied Earth Observation and Geoinformation, 8:173-187.
37. Mather, P.M. (1999) Computer processing of remotely sensed images, 2nd edn. Wiley, Chichester.
38. Mandal R. A. and Laake P. van. 2005. Carbon sequestration in community forests: an eligible issue for CDM (A case study of Nainital, India), Banko Janakari, 15:53-61.
39. Mani, S., Parthasarathy, N. 2007. Above-ground biomass estimation in ten tropical dry evergreen forest sites of peninsular India, Biomass and Bioenergy, 31: 284-290.
40. Martinez-Yrizar, A., Maass, J. M., Perez-Jimenez, L. A., Sarukhan, J. 1996. Net Primary Productivity of a Tropical Deciduous Forest Ecosystem in Western Mexico, Journal of Tropical Ecology, 12:169-175.
41. Mohns B., Applegate G.B., Gilmour D.A. 1988. Biomass and productivity estimations for community forest management: A case study from the Hills of Nepal – II. Dry matter production in mixed young stands of chir pine (Pinus roxburghii) and broad-leaved species. Biomass. 17:165-184.
42. Murali K.S., Bhat D.M. and. Ravindranath N.H. 2005. Biomass estimation equation for tropical deciduous and evergreen forests, International Journal of Agricultural Resources, Governance and Ecology,  4:81–92.
43. Murali K.S., Bhat D.M., Ravindranath N.H. 2000. Biomass Estimation Equations for Tropical Deciduous and Evergreen Forests. Centre for Ecological Sciences, Indian Institute of Science, Technical Report - 81.
44. Nascimento, H. E. M., Laurance, W. F. 2002. Total aboveground biomass in central Amazonian rainforests: a landscape-scale study, Forest Ecology and Management, 168:311-321.
45. Negi, A. K. Todaria, N. P. 1993. Studies on the impact of local folk on forests of Garhwal Himalaya. 1: Energy from biomass, Biomass and Bioenergy. 4:447-454.
46. Negi, K. S., Y. S. Rawat, and J. S. Singh. 1983. Estimation of biomass and nutrient storage in a Himalayan moist temperate forest. Canadian Journal of Forest Research 13: 1185-1196.
47. Northup B.K., Zitzer S.F., Archer S., McMurtry C.R., Boutton T.W. 2005. Above-ground biomass and carbon and nitrogen content of woodyspecies in a subtropical thornscrub parkland. Journal of Arid Environments. 62: 23–43
48. Olson J.S, Watts J.A, and Allison L.J, 1983, Carbon of Live vegetation of world ecosystem, National technical informative service, Springerfield.
49. Patenaude G, R Milne, TP Dawson, 2005, Synthesis of remote sensing approaches for forest carbon estimation: reporting to the Kyoto Protocol, Environmental Science and Policy, Volume 8, Issue 2, pp 161-178
50. Rai, S. N. 1984. Above ground biomass in tropical rainforests of Western Ghats. Indian For. 110:754–764.
51. Rai, S.N. and Proctor, J. 1986. Ecological studies on four forests in Karnataka, India. I. Environment, structure, floristics and Biomass, Journal of Ecology. 74:439–454.
52. Ramachandra T.V, Kamakshi B, Shruthi B.V. 2004. Bioresources status in Karnataka, Renewable And Sustainable Energy Reviews, 8:1-47
53. Rana B.S., Singh S.P. and Singh R.P. 1989. Biomass and Net Primary Productivity in Central Himalayan Forests along an Altitudinal Gradient, Forest Ecology and Management. 27:199-218.
54. Ravindranath N.H, M.R.Mohan Nayak, R.S Hariyur, and C.R Dinesh, 1991, The status of Tree biomass in a Semi arid Ecosystem, Biomass and Bioenergy  Vol. I, No. I, pp. 9-16,
55. Rawat, Y. S., and J. S. Singh. 1988. Structure and function of oak forests in Central Himalaya. I. Dry matter dynamics. Annals of Botany 62:397-4 1 I.
56. Ripple W.J, 1985,  Asymptotic reflectance characteristics of grass vegetation, photogrammetric Engineering and Remote Sensing. Vol. 51, pp. 1915-1921
57. Ringrose, S., Matheson, W., Matlala, C.J.S.S., O'Neill, T. & Werner, P.A. (1994) Vegetation spectral reflectance along a north-south vegetation gradient in northern Australia. JournalofBiogeography, 21, 33-47
58. Sharma, E., Sundriyal, R.C., Rai, S.C., Bhatt, Y.K., Rai, L.K., Sharma. R. and Rai, Y.K., 1992. Integrated watershed management: A case study in Sikkim Himalaya. Gyanodaya Prakashan. Nainital, 120 pp.
59. Sharma.M. 1996. Current environmental problems and future perspectives. Tropical Ecology, 37:15–20
60. Sierra Carlos A., Valle Jorge I. del, Orrego Sergio A., Moreno Flavio H., Harmon Mark E., Zapata Mauricio, Colorado Gabriel J., Herrera Marı´a A., Lara Wilson, Restrep David E. o, Berrouet Lina M, Loaiza Lina M., Benjumea John F. 2007. Total carbon stocks in a tropical forest landscape of the Porce region, Colombia, Forest Ecology and Management, 243:299-309.
61. Singh Arvind, Jha A.K. & Singh J.S. 1997. Influence of a developing tree canopy on the yield of Pennisetum pedicellatum sown on a mine spoil, Journal of Vegetation Science, 8:537-540.
62. Singh Surendra P, Adhikari Bhupendra S., Zobel Donald B. 1994. Biomass, Productivity, Leaf Longevity, and Forest Structure in the Central Himalaya, Ecological Monographs, 64: 401-421.
63. Singh Lalji and Singh J.S 1991, Species Structure, Dry Matter Dynamics and Carbon Flux of a Dry Tropical Forest in India, Annals of Botany 68: 263-273
64. Sundriyal R.C., Sharma E. 1996. Anthropogenic pressure on tree structure and biomass in the temperate forest of Mamlay watershed in Sikkim , Forest Ecology and Management,  81: 113-134
65. Sundriyal, R.C., Sharma, E., Rai, L.K. and Rai, S.C. 1994. Tree structure, regeneration and woody biomass removal in a subtropical forests of Mamaly watershed in the Sikkim Himalaya. Vegetation, 113: 53-63.
66. Swamy SL, A Mishra, S Puri, 2006, Comparison of growth, biomass and nutrient distribution in five promising clones of Populus deltoides under an agrisilviculture system, bioresources Technology, Volume 97, Issue 1: pp 57-68
67. Tiwari A.K. 1992. Component – wise biomass models for trees: A non-Harvest technique, Indian for, 118: 405-410.
68. Wang Chuankuan. 2005. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests, Forest Ecology and Management. 222: 9–16.
69. Westman, W. E. Whittaker, R. H.1975. The Pygmy Forest Region of Northern California: Studies on Biomass and Primary Productivity, Journal of Ecology, 63:490-520.
70. Whittaker, R. H., Woodwell, G. M. 1968. Dimension and Production Relations of Trees and Shrubs in the Brookhaven Forest, New York. Journal of Ecology, 56:1-25
71. Whittaker, R. H., Woodwell, G. M.1969. Structure, Production and Diversity of the Oak-Pine Forest at Brookhaven, New York, Journal of Ecology,  55: 155-174
72. Whittaker, R. H. Niering, W. A.1975. Vegetation of the Santa Catalina Mountains, Arizona. V. Biomass, Production, and Diversity along the Elevation Gradient, Ecology; 56:771-790
73. Whittaker, R. H.1996. Forest Dimensions and Production in the Great Smoky Mountains, Ecology; 47:103-121
74. Xiao Chun-Wang, Ceulemans R. 2004. Allometric relationships for below- and aboveground biomass of young Scots pines, Forest Ecology and Management, 203: 177–186.
75. https://classes.yale.edu/05-06/fes519b/methods-006/FES_519_Spring_2006/ Biomass_objectives.html Last accessed on 9 May 2007

BACK  «  TOP  »  NEXT