 |
Assimilation of Endmember Variability in Spectral Mixture Analysis for Urban Land Cover Extraction
|
 |
1Energy and Wetlands Research Group, Centre for Ecological Sciences [CES], 2Department of Management Studies, 5Centre for Sustainable Technologies (astra),
6Centre for infrastructure, Sustainable Transportation and Urban Planning [CiSTUP],
Indian Institute of Science, Bangalore – 560012, India.
3International Institute of Information Technology (IIITB), Bangalore-560100, India.
4EADS Innovation Works, Airbus Engineering Centre India, Xylem No 4, Mahadevapura Post, Whitefield Road, Bangalore - 560 048, India.
*Corresponding author: cestvr@ces.iisc.ac.in
|
Linear model
Linear unmixing assumes that a satellite signal is modeled as a weighted sum of a limited number of basic signals, where each of these signals is characteristic of one of a number of LC types contributing to the signal. If there are M spectral bands and N classes, then associated with each pixel is a M-dimensional vector y whose components are the gray values corresponding to the M bands. Let E = [e1, …,en-1, en, en+1, . . , eN] be a M × N matrix, where {en} is a column vector representing the spectral signature (endmember) of the nth target material. For a given pixel, the abundance or fraction of the nth target material present in a pixel is denoted by αn, and these values are the components of the N-dimensional abundance vector α. Assuming LMM (Shimabukuro and Smith, 1991), the observation vector 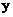 is related to E by is related to E by
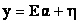 (1) (1)
where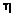 accounts for the measurement noise. We further assume that the components of the noise vector accounts for the measurement noise. We further assume that the components of the noise vector 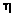 are zero-mean random variables that are i.i.d. (independent and identically distributed). Therefore, the covariance matrix of the noise vector is σ2I, where σ2 is the variance, and I is M × M identity matrix. Two constraints imposed on the abundances in Eq. (1) are the non-negativity and sum-to-one given as are zero-mean random variables that are i.i.d. (independent and identically distributed). Therefore, the covariance matrix of the noise vector is σ2I, where σ2 is the variance, and I is M × M identity matrix. Two constraints imposed on the abundances in Eq. (1) are the non-negativity and sum-to-one given as
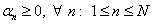 (2) (2)
and
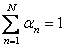 (3) (3)
This allows proportions of each pixel to be partitioned between classes.The conventional approach (Nielsen, 2001) to extract the abundance values is to minimise 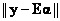 , and the Unconstrained Least Squares estimate for the abundance is , and the Unconstrained Least Squares estimate for the abundance is
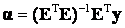 . (4) . (4)
Imposing the unity constraint on the abundance values while minimising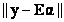 , gives the Constrained Least Squares (CLS) estimate of the abundance as, , gives the Constrained Least Squares (CLS) estimate of the abundance as,
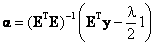 (5) (5)
where
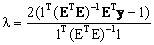 . (6) . (6)
|
|
Citation : Uttam Kumar, S. Kumar Raja, Chiranjit Mukhopadhyay and T.V. Ramachandra., 2013, Assimilation of endmember variability in spectral mixture analysis for urban land cover extraction., Advances in Space Research, Volume 52, Issue 11, 1 December 2013, Pages 2015-2033.
|


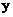 is related to E by
is related to E by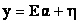 (1)
(1)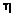 accounts for the measurement noise. We further assume that the components of the noise vector
accounts for the measurement noise. We further assume that the components of the noise vector 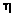 are zero-mean random variables that are i.i.d. (independent and identically distributed). Therefore, the covariance matrix of the noise vector is σ2I, where σ2 is the variance, and I is M × M identity matrix. Two constraints imposed on the abundances in Eq. (1) are the non-negativity and sum-to-one given as
are zero-mean random variables that are i.i.d. (independent and identically distributed). Therefore, the covariance matrix of the noise vector is σ2I, where σ2 is the variance, and I is M × M identity matrix. Two constraints imposed on the abundances in Eq. (1) are the non-negativity and sum-to-one given as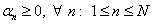 (2)
(2)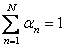 (3)
(3)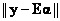 , and the Unconstrained Least Squares estimate for the abundance is
, and the Unconstrained Least Squares estimate for the abundance is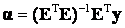 . (4)
. (4)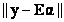 , gives the Constrained Least Squares (CLS) estimate of the abundance as,
, gives the Constrained Least Squares (CLS) estimate of the abundance as,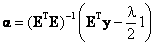 (5)
(5)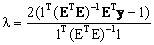 . (6)
. (6)