|
Conceptual framework for Variable Endmember Constrained Least Square (VECLS)
Intra-class variability of remotely sensed data is often too high or too low for unmixing a single pixel (Petrou & Foschi, 1999). In such situations, the endmember of a particular class are not strictly unique vectors and there is always a variation within that class. Therefore, we modify Eq. (1) to represent variable endmembers as random vectors, and introduce the following statistical LMM
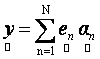 (7) (7)
where,  is the observed set of M reflectance values and is the observed set of M reflectance values and 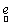 is the random vector representing the variable endmember of class n. The endmembers of each class n are drawn from a probability distribution defined by the probability density function (p.d.f.) is the random vector representing the variable endmember of class n. The endmembers of each class n are drawn from a probability distribution defined by the probability density function (p.d.f.)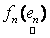 . It is reasonable to make an assumption that endmemberp.d.f.s of distinct LC categories are mutually independent. For example, the spectral signature distribution of builtup and vegetation can be treated independently. As a consequence of the above assumption, . It is reasonable to make an assumption that endmemberp.d.f.s of distinct LC categories are mutually independent. For example, the spectral signature distribution of builtup and vegetation can be treated independently. As a consequence of the above assumption, 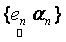 are also mutually independent. If we denote are also mutually independent. If we denote 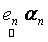 as as 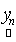 , Eq. (7) can be rewritten as , Eq. (7) can be rewritten as
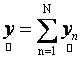 (8) (8)
andp.d.f. of 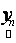 can be shown to be can be shown to be 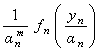 . Since { . Since {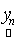 } are mutually independent, p.d.f. of } are mutually independent, p.d.f. of 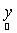 is given by is given by
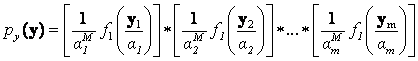 , (9) , (9)
where, * denotes a convolution operator.Note that p.d.f. of 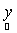 implicitly depends on the abundance values implicitly depends on the abundance values 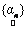 . Given the observation vector y, we define the likelihood function L as . Given the observation vector y, we define the likelihood function L as
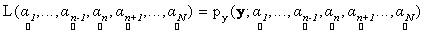 . (10) . (10)
Here, we estimate abundance values by seeking 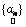 which maximises the likelihood function subject to the constraint that sum of all abundance values add to 1, which is the value of which maximises the likelihood function subject to the constraint that sum of all abundance values add to 1, which is the value of 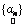 that maximises the likelihood function. This means, given that maximises the likelihood function. This means, given 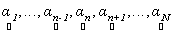 , , 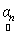 is the value for which is the value for which  has the maximum chance to occur. Also note that abundance values are deterministic quantities. has the maximum chance to occur. Also note that abundance values are deterministic quantities.
We first assume a Gaussian case and then subsequently move on to a generalised case, where the form of p.d.f. is not assumed. Let 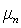 and and 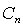 be mean vector and covariance of nth target material, respectively. It is clear from LMM in Eq. (7) that the distribution of observation ( be mean vector and covariance of nth target material, respectively. It is clear from LMM in Eq. (7) that the distribution of observation (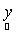 ) is also Gaussian whose mean and covariance are given by ) is also Gaussian whose mean and covariance are given by
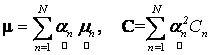 . (11) . (11)
In our framework, in order to find the ML (Maximum Likelihood) abundances, we maximise the log-likelihood
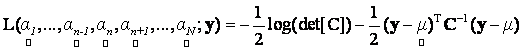 (12) (12)
The above approach is based on the assumption that the underlying distribution of the spectral signatures are normal.
Next, in what follows we show a framework where no assumption on the form of p.d.f. is made. Let Z be a matrix whose column are the means of the spectral signatures i.e., 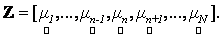 Suppose that the actual observation is o, then we seek to minimise the deviation between o and Suppose that the actual observation is o, then we seek to minimise the deviation between o and 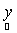 subject to constraints given in Eq. (3). We minimise, subject to constraints given in Eq. (3). We minimise,
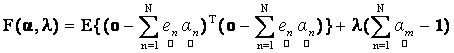 (13) (13)
where, E{.} is the expectation operator and λ is the Lagrangian multiplier for enforcing the constraint on the abundance. Using (11), it is easy to simplify the expectation term in expression (13) as follows:
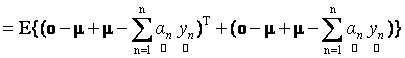 (14) (14)
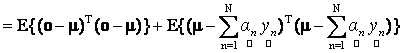 (15) (15)
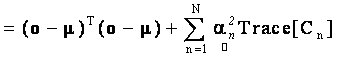 . (16) . (16)
Note that in Eq. (16) no cross-correlation terms appear. Denoting V as the diagonal matrix whose nth diagonal element is the trace of 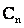 (covariance of nth target material), the objective function F(α) can be written in a more compact form using Z and V as (covariance of nth target material), the objective function F(α) can be written in a more compact form using Z and V as
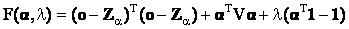 (17) (17)
where 1 is a vector whose components are all 1. In order to find the minima, we first take the first derivative of F(α) with respect to 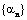 , λ and equate it to 0. , λ and equate it to 0.
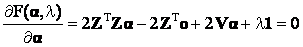 (18) (18)
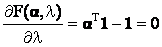 (19) (19)
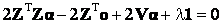
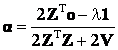 (20) (20)
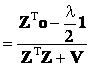
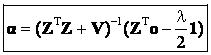 . (21) . (21)
Now we derive an explicit expression for λ. Denoting 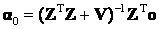 , Eq. (20) can be written as , Eq. (20) can be written as
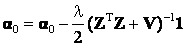 (22) (22)
Multiplying 1T on both sides, we get
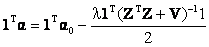 . (23) . (23)
Note that 1Tα = 1. Therefore the final expression for λ is
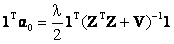 (24) (24)
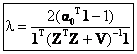 (25) (25)
In conventional approach, where the endmembers are assumed to be constant, Z represents the endmember matrix (V=0), and the endmembers are obtained by minimising
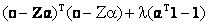 (26) (26)
subject to the constraint that 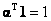 . However, in this approach, we have assumed the endmembers to be variable, and as a consequence the endmember variability term namely V has been accounted. . However, in this approach, we have assumed the endmembers to be variable, and as a consequence the endmember variability term namely V has been accounted.
The spectral mixture analysis (SMA) techniques for addressing endmember variability have been broadly categorised (Somers et al., 2011) based on five basic principles: (i) iterative mixture analysis cycle, (ii) spectral feature selection, (iii) spectral weighting, (iv) spectral transformations, and (v) spectral modelling. Table 1 compares VECLS with the existing techniques (Somers et al 2011) and it is evident that VECLS is conceptually different as VECLS is not iterative, does not involve spectral feature selection, spectral weighting, spectral transformation or even spectral modelling. Hence VECLS has been placed as a separate category in the table for comparison. The underlying genesis behind the methods, advantages and disadvantages are also highlighted.
Table 1: Comparative analysis of the existing endmember variability spectral mixture analysis techniques with VECLS.
| Sl. No. |
Basic Principle |
Techniques |
Genesis |
Advantage |
Disadvantage |
Observation |
| 1 |
Iterative mixture analysis cycle |
MESMA (Multiple Endmember Spectral Mixture Analysis,(Roberts et al., 1998)) |
MESMA allows multiple endmember for each component. |
- Endmembers are allowed to vary onpixel basis.
- Each plausible endmember is accounted by assigning a best-fit (lowest RMSE) to each pixel iteratively.
|
High computation complexity because of iterative nature of the method. |
Iterative mixture analysis leads to more than one possible combination of pure spectra and sometimes results in the same mixed spectrum which is a ill posedness problem. |
| Auto MCU (Monte Carlo Spectral Unmixing Model, (Asner and Lobell, 2000)) |
A large number of endmember combinations for each pixel are calculated by randomly selecting spectra from a spectral database to unmix a pixel (also called fuzzy unmixing). |
The number of model samples for each of the possible mixture combination is used to compute the probability and confidence of each mixture. |
It propagates uncertainity in the endmember spectra to the final subpixel cover fraction results. |
| Endmember Bundles (Bateson et al., 2000) |
- From the eigenvectors (obtained through Principal Component Analysis) of the image, bundles of vectors are identified to represent the endmembers.
- A linear programming routine determines minimum, mean and maximum fraction of each endmember.
|
|
|
| BSMA (Bayesian Spectral Mixture Analysis, (Song, 2005)) |
BSMA is based on Bayes theorem.It unmixes each pixel with randomly selected combination of endmembers which are represented by a p.d.f. |
- Accounts for the probability of spectral signatures instead of assuming equal probabilities for all endmembers.
- Captures spectral variability with least number of endmembers.
|
SMA gives subpixel fractions with almost the same and
sometimes even better accuracy than BSMA where uncertainty information for the estimates is the exception. |
| 2 |
Spectral feature selection (SFS) |
- AutoSWIR (Asner&Lobell, 2000)
- Residual Analysis based SFS (Ball et al., 2007)
- PCA based SFS (Miao et al., 2006)
- DCT based SFS ( Li, 2004)
- SZU based SFS (Somers et al., 2010b)
|
- Based on data reduction by selection of wavelengths.
- It is robust against spectral variability i.e. it minimises intra and maximises inter-class variability.
|
- Computation complexity is reduced because of data dimensionality reduction.
- Incorporates uncorrelated spectral information.
- AutoMCU includes both VIS and NIR bands for feature selection, thereby covering wider wavelength region.
|
AutoSWIR is completely dependent on the availability of high-fidelity SWIR2 region; originally designed for semi-arid region which may not be always true. |
SZU was found to be better than AutoSWIR and MESMA. |
| 3 |
Spectral weighting |
Spectral weighting based technique by Somers et al., (2009b) |
- It prioritises spectral bands less sensitive to endmember variability by giving them higher weight in spectral mixture analysis.
- The estimated cover fractions are influenced or determined by high reflected energy level in the reflectance bands of the pixel.
|
The highest reflectance bands for each object can be easily used to estimate class proportions with higher accuracy. |
Assigning weightage to endmembers based on dominating wavebands may sometimes be nontrivial. |
For vegetation studies, NIR band will dominate the model and VIS bands will dominate marginally. |
| 4 |
Spectral transformations (ST) |
- Tied Spectrum based ST (Asner and Lobell, 2000).
- Normalised Spectral Mixture Analysis (NSMA, Wu, 2004).
- Derivative Spectral unmixing (DSU, Zhang et al., 2004).
- First derivative based ST (Debba et al., 2006).
- Wavelet based ST (Li, 2004).
|
Instead of original reflectance data, transformed / modified spectral information is used for spectral unmixing. |
- Landscape features gets highlighted because of spectral band transformation.
- Endmemberseparability increases.
|
Careful calibration / validation may be required (example, for DSU), as derivatives increase SNR. |
Two different transformation methods on the same data may not produce consistent class proportion results such as derivative and wavelet because the number of spectral bands for analysis is only a subset of the original full spectral range. |
| 5 |
Spectral modelling |
- Weighted Linear Spectral Mixture Analysis (Example: Soil Modeling Mixture Analysis - SMMA by Somers et al., 2009a).
- MODTRAN radiative transfer model (Eckmann et al., 2008).
|
Radiative transfer models are used to generate endmember libraries for spectral mixture analysis. |
They provide dynamic and robust way to account the spatial and temporal variability. |
Each model is specific to an application and cannot be generalised. |
SMMA cannot work for a landscape which has no soil. |
| 6 |
Variable Endmember Constrained Least Square (VECLS) |
- Allows the signals within a class to vary from pixel to pixel about a mean spectrum.
- Endmembers are selected both automatically (through N-FINDR) and using supervised techniques.
- Through many instances of a particular endmember, its variability and the inter-class variance are accounted by the covariance around the selected endmember mean.
|
- Non-iterative so less computation complexity.
- Method does not involve feature selection, spectral weighting, and transformations.
- It is not designed for any specific endmember mixture model and is separately derived for a Gaussian and a generalised case (no assumption of the form of p.d.f.).
|
- The method is applied on simulated and an urban landscape. Its performance on different landscapes has to be assessed to understand the robustness of the technique.
|
The method needsto be applied on different datasets such as hyperspectral with higher number of classes to assess its utility. |
|


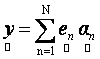 (7)
(7) is the observed set of M reflectance values and
is the observed set of M reflectance values and 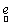 is the random vector representing the variable endmember of class n. The endmembers of each class n are drawn from a probability distribution defined by the probability density function (p.d.f.)
is the random vector representing the variable endmember of class n. The endmembers of each class n are drawn from a probability distribution defined by the probability density function (p.d.f.)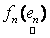 . It is reasonable to make an assumption that endmemberp.d.f.s of distinct LC categories are mutually independent. For example, the spectral signature distribution of builtup and vegetation can be treated independently. As a consequence of the above assumption,
. It is reasonable to make an assumption that endmemberp.d.f.s of distinct LC categories are mutually independent. For example, the spectral signature distribution of builtup and vegetation can be treated independently. As a consequence of the above assumption, 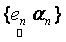 are also mutually independent. If we denote
are also mutually independent. If we denote 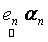 as
as 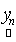 , Eq. (7) can be rewritten as
, Eq. (7) can be rewritten as 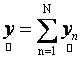 (8)
(8)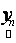 can be shown to be
can be shown to be 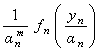 . Since {
. Since {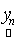 } are mutually independent, p.d.f. of
} are mutually independent, p.d.f. of 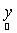 is given by
is given by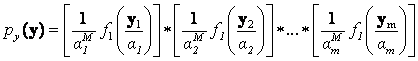 , (9)
, (9)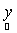 implicitly depends on the abundance values
implicitly depends on the abundance values 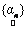 . Given the observation vector y, we define the likelihood function L as
. Given the observation vector y, we define the likelihood function L as 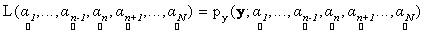 . (10)
. (10)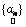 which maximises the likelihood function subject to the constraint that sum of all abundance values add to 1, which is the value of
which maximises the likelihood function subject to the constraint that sum of all abundance values add to 1, which is the value of 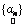 that maximises the likelihood function. This means, given
that maximises the likelihood function. This means, given 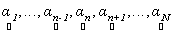 ,
, 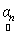 is the value for which
is the value for which  has the maximum chance to occur. Also note that abundance values are deterministic quantities.
has the maximum chance to occur. Also note that abundance values are deterministic quantities.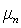 and
and 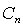 be mean vector and covariance of nth target material, respectively. It is clear from LMM in Eq. (7) that the distribution of observation (
be mean vector and covariance of nth target material, respectively. It is clear from LMM in Eq. (7) that the distribution of observation (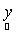 ) is also Gaussian whose mean and covariance are given by
) is also Gaussian whose mean and covariance are given by 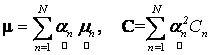 . (11)
. (11)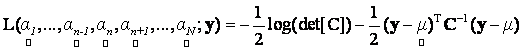 (12)
(12)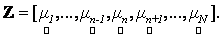 Suppose that the actual observation is o, then we seek to minimise the deviation between o and
Suppose that the actual observation is o, then we seek to minimise the deviation between o and  subject to constraints given in Eq. (3). We minimise,
subject to constraints given in Eq. (3). We minimise,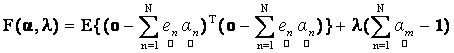 (13)
(13)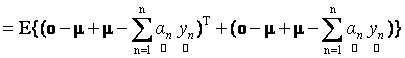 (14)
(14)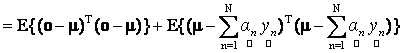 (15)
(15)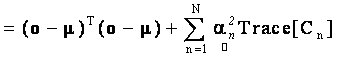 . (16)
. (16)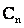 (covariance of nth target material), the objective function F(α) can be written in a more compact form using Z and V as
(covariance of nth target material), the objective function F(α) can be written in a more compact form using Z and V as 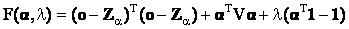 (17)
(17)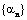 , λ and equate it to 0.
, λ and equate it to 0.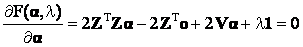 (18)
(18) 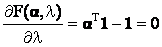 (19)
(19) 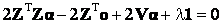
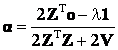 (20)
(20)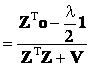
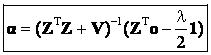 . (21)
. (21)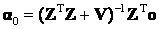 , Eq. (20) can be written as
, Eq. (20) can be written as 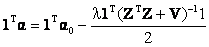 . (23)
. (23)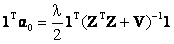 (24)
(24)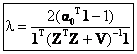 (25)
(25)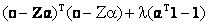 (26)
(26)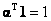 . However, in this approach, we have assumed the endmembers to be variable, and as a consequence the endmember variability term namely V has been accounted.
. However, in this approach, we have assumed the endmembers to be variable, and as a consequence the endmember variability term namely V has been accounted.