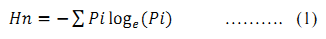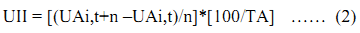|
Method
Figure 2 outlines the method adopted for analysing multi-resolution remote sensing data. Landsat data acquired were geo-corrected with the help of known ground control points (GCP’s) collected from the Survey of India topo-sheets and Global Positioning System (GPS). ETM+ data was corrected for SLC-off defect. Geo corrected data is then resampled to 30 meter in order to maintain a common resolution across all the data sets.
The data was classified into four land use categories - urban, vegetation, water bodies and others (open space, barren land, etc.) with the help of training data using supervised classifier – Gaussian maximum likelihood classifier (GMLC). This preserves the basic land use characteristics through statistical classification techniques using a number of well-distributed training pixels. Grass GIS (http://wgbis.ces.iisc.ac.in/grass/index.php), free and open source software with robust support of processing both vector and raster data has been used for this analysis. Possible errors during spectral classification are assessed by a set of reference pixels. Based on the reference pixels, statistical assessmentof classifier performance including confusion matrix, kappa (κ) statistics and producer's and user's accuracies were calculated. These accuracies relate solely to the performance of spectral classification.Infill, linear, clustered, expansion, scattered are considered as different growth types in this study. Infill development is usually referred as compact development. Infill development converts vacant or unutilized urban land into higher density development. Infill is means of accommodating the growth within urban area's geographical extent. Growth of the urban is modeled by a fixed amount of changes for each time period referred as linear growth. The expansion of a community without concern for consequences and expanded around their peripheries that forms a new agglomeration termed as high expansion or clustered growth. Scattered development is a low density development, growth of urban area increases dramatically in short time span with new development activities in the periphery.
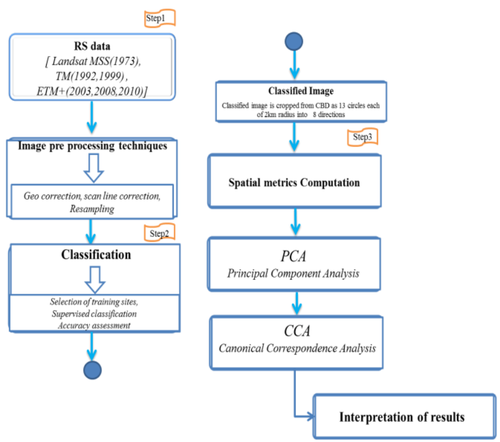
Fig. 2 Method tailed to understand urban landscape change
Analysis of urban sprawl
Urban sprawl refers to the disaggregated or dispersed growth at outskirts and these localities are devoid of basic amenities (drinking water, sanitation, etc.). This necessitates understanding sprawl process for effective regional planning. The location factors, such as distance to urban center and roads act as catalyst for urban sprawl. Shannon’s entropy given in equation 1 has been used to measure the extent of urban sprawl with remote sensing data [37], [38]. Shannon’s entropy was calculated across all directions to analyse the extent of urbanisation
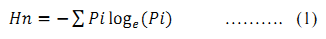
Where, Pi is the Proportion of the variable in the ith zone and n is the total number of zones. This value ranges from 0 to log n, indicating very compact distribution for values closer to 0. The values closer to log n indicates that the distribution is much dispersed. Larger value (close to log n) indicates fragmented growth indicative of sprawl.
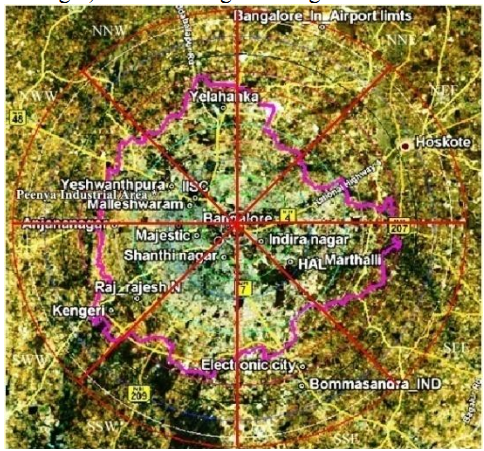
Fig. 3 Study area with important landmarks (source: Google Earth)
Analysis of spatial patterns of urbanisation - computation of Landscape metrics
The gradient based approach is adopted to explain the spatial patterns of urbanisation. The study region, given in Figure 3 was divided into eight zones based on the directions, which were further divided into concentric circles (13 circles) with incrementing radius of 2 kilometer. Landscape metrics were computed for each region to understand the landscape dynamics at local levels due to urbanisation.
A Spatio-temporal pattern of the landscape is understood through landscape metrics. These spatial metrics are a series of quantitative indices representing physical characteristics of the landscape mosaic. Table 1 (Appendix I) lists the indicators that reflect the landscape’s spatial and temporal changes [5], [16], [39], [40]. Thesemetrics are grouped into the five categories: Patch area metrics, Edge/border metrics, Shape metrics, Compactness/ contagion / dispersion metrics, Open Space metrics.
Analysis of land use expansion – computation of Urban Intensity Index (UII):
Urban Intensity Index (UII) is used to compare the intensity of land use expansion at different time periods. UII results in the normalization of the land area in various spatial units divided by the annual rate of expansion [41]. UII is the percentage of expansive area of urban land use in the total area and is given by 2.
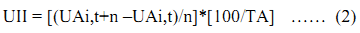
Where UA is urban area per year of spatial unit i, urban land use area of year t+n, land use of year t and TA resembles total land area;n represents the number of years.
|