|
Methodology
Automatic endmember extraction – The N-FINDR algorithm – N-FINDR is a fully automatic technique for endmember selection [13] as briefed below:
- Let P denote the number of classes or endmembers to be identified.
- Perform a Principal Component Analysis (PCA)-decomposition of the data and reduce the dimension of the data to P - 1. In what follows, we assume that the data is transformed to P - 1 dimension PCA space.
- Pick P pixels from the set and compute the simplex volume generated by the spectra of the P pixels.
- Replace each endmember with the spectrum of each pixel in the data set and recompute the simplex volume. If the volume increases, the spectrum of the new pixel is retained as a potential endmember.
The above steps are executed iteratively considering all the pixels, and the final set of spectra retained is taken to be the endmembers.
Orthogonal subspace projection (OSP) – In order to solve the linear part of the mixing problem, we used OSP [14]. OSP is based on two aspects: 1) how to best utilise the target knowledge provided a priori and 2) how to effectively make use of numerous spectral bands. Assuming the LMM, the observation vector y is related to E by
 . (2) . (2)
We further assume that the components of the noise vector  are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is 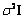 , where , where  is the variance, and I is K x K identity matrix. is the variance, and I is K x K identity matrix.
The conventional approach [15] to extract the abundance values is to minimise  , and the estimate for the abundance is , and the estimate for the abundance is
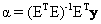 (3) (3)
which is termed as the Unconstrained Least Squares (ULS) estimate of the abundance. Imposing the sum-to-one constraint on the abundance values, gives the Constrained Least Squares (CLS) estimate of the abundance as,
 (4) (4)
where,
 . (5) . (5)
In order to find the abundance of the pth target material (αp), let the corresponding spectral signature of the desired target material be denoted as d. The term Eα in (2) can be rewritten to separate the desired spectral signature d from the rest as:
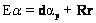 (6) (6)
where r contains the abundance of the rest of the end-members, and R is a (K x P– 1) matrix containing the columns of E except for the column vector d. We rewrite (2) as
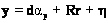 . (7) . (7)
The interfering signatures present in R can be removed from (7) by the operator,
 (8) (8)
which is used to project the vector  into a space orthogonal to the space spanned by the interfering spectral signatures. Therefore, operating on y with P, and noting that PR = 0, into a space orthogonal to the space spanned by the interfering spectral signatures. Therefore, operating on y with P, and noting that PR = 0,
 . (9) . (9)
The next step is to find an operator wT which maximises the SNR given by
 (10) (10)

Maximising the SNR leads to the generalised eigenvalue problem: 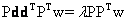 . The eigenvector corresponding to the maximum eigenvalue is the vector ‘w’. It can be shown that the w which maximises the SNR is given by . The eigenvector corresponding to the maximum eigenvalue is the vector ‘w’. It can be shown that the w which maximises the SNR is given by
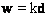 . (11) . (11)
Therefore, an optimal estimate of αp is given by
 (12) (12)
In the absence of noise, the estimate matches with the exact value as in (7). The value of α is the abundance of the pth class (in an abundance map) ranging from 0 to 1 in any given pixel. 0 indicates absence of a particular class and 1 indicates full presence of that class in that particular pixel.
ANN based multi-layer perceptron (MLP) – The advent of ANN approaches is mainly due to their power in pattern recognition, interpolation, prediction, forecasting, classification and process modeling [16]. A MLP network comprises a number of identical units organised in layers, with those on one layer connected to those on the next layer so that the output of one layer are used as input to the next layer.
A detailed introduction on MLP can be found in literatures [16-19]. The main aspects here are: (i) the order of presentation of training samples should be randomised from epoch to epoch; and (ii) the momentum and learning rate parameters are typically adjusted (and usually decreased) as the number of training iterations increases. |


 . (2)
. (2) are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is
are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is 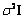 , where
, where  is the variance, and I is K x K identity matrix.
is the variance, and I is K x K identity matrix. , and the estimate for the abundance is
, and the estimate for the abundance is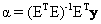 (3)
(3) (4)
(4) . (5)
. (5)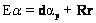 (6)
(6) 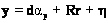 . (7)
. (7) (8)
(8)  into a space orthogonal to the space spanned by the interfering spectral signatures. Therefore, operating on y with P, and noting that PR = 0,
into a space orthogonal to the space spanned by the interfering spectral signatures. Therefore, operating on y with P, and noting that PR = 0, . (9)
. (9) (10)
(10)
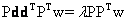 . The eigenvector corresponding to the maximum eigenvalue is the vector ‘w’. It can be shown that the w which maximises the SNR is given by
. The eigenvector corresponding to the maximum eigenvalue is the vector ‘w’. It can be shown that the w which maximises the SNR is given by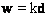 . (11)
. (11)  (12)
(12)