 |
A Multi-layer Perceptron based Non-linear Mixture Model to estimate class abundance from mixed pixels |
 |
Uttam Kumar1, 2, S. Kumar Raja5, C. Mukhopadhyay1 and T.V. Ramachandra2, 3, 4, *
Senior Member, IEEE
1 Department of Management Studies, 2 Centre for Sustainable Technologies, 3 Centre for Ecological Sciences,
4 Centre for infrastructure, Sustainable Transport and Urban Planning, Indian Institute of Science, Bangalore – 560012, India.
5 Institut de Recherche en Informatique et Systèmes Aléatoires, 35042 Rennes cedex - France & Technicolor Research & Innovation, Cesson Sévigné, France.
*Corresponding author: cestvr@ces.iisc.ac.in
|
|
|
|
Computer simulations
One of the major problems involved in analysing the quality of fractional estimation methods is the fact that ground truth information about the real abundances of materials at sub-pixel levels is difficult to obtain in real scenarios [21]. In order to avoid this shortcoming, simulation of hyperspectral imagery was carried out to examine the algorithm’s performance in a controlled manner.
Spectral libraries of four minerals - alunite, buddingtonite, kaolinite and calcite (available at http://speclib.jpl.nasa.gov/) were used to generate synthetic data. Plaza et al. [21], used the signatures of soil (e1) and vegetation (e2) to create a simulated image with non-linear mixtures using a simple logarithmic function. The abundance of e1 and e2 were assigned according to (14)
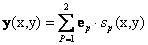 (14) (14)
where, y denotes a vector containing the simulated discrete spectrum of the pixel at spatial coordinates (x,y) of the simulated image, 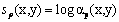 is the contribution of endmember ep and is the contribution of endmember ep and 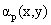 is the fractional abundance of ep at (x,y). A limitation here is that even though all the pixels are mixed in different proportions, there are no instances of pure pixels. If α is 1, we expect the observed hyperspectral signature to be solely from one material, and therefore, ideally it should be identical to the endmember itself. Here, as the abundance increases towards 1, log (α) approaches 0, thereby suppressing the contribution of that particular endmember. On the other hand, if α is 0, log (α) approaches is the fractional abundance of ep at (x,y). A limitation here is that even though all the pixels are mixed in different proportions, there are no instances of pure pixels. If α is 1, we expect the observed hyperspectral signature to be solely from one material, and therefore, ideally it should be identical to the endmember itself. Here, as the abundance increases towards 1, log (α) approaches 0, thereby suppressing the contribution of that particular endmember. On the other hand, if α is 0, log (α) approaches 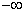 , and therefore, starts dominating in the observed spectral signature. Of course, it will appear as negative numbers. This is against our physical understanding as to how a material which is almost not present in the pixel, contribute to the observation in a dominant way? That is, the model is not able to highlight the endmember of the correct material when its contribution is 1 and gives a wrong endmember when its contribution is 0. To overcome this limitation, we modify the model in (14) by (15): , and therefore, starts dominating in the observed spectral signature. Of course, it will appear as negative numbers. This is against our physical understanding as to how a material which is almost not present in the pixel, contribute to the observation in a dominant way? That is, the model is not able to highlight the endmember of the correct material when its contribution is 1 and gives a wrong endmember when its contribution is 0. To overcome this limitation, we modify the model in (14) by (15):
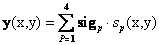 (15) (15)
where,  is the signature corresponding to pth mineral, is the signature corresponding to pth mineral,  is the contribution of endmember ep and is the contribution of endmember ep and 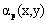 is the fractional abundance of ep in the pixel at (x,y). is the fractional abundance of ep in the pixel at (x,y).
Simulated synthetic non-linear mixture hyperspectral data of 200 bands (250 x 250) using four minerals were classified using Maximum Likelihood Classifier (MLC) with signatures from the spectral libraries. This constitutes high-resolution (HR) images. These images were used to generate synthetic mixed pixels of 25 x 25 (referred as low-resolution - LR images). Four endmembers were extracted from LR images, and subsequently, abundance images were estimated corresponding to each endmember. Percentage abundance for a group of 10 x 10 pixels were computed for this entire HR classified image (250 x 250) obtained from MLC. This new image of size 25 x 25 was used as reference for validating the LR abundance output. However, the HR MLC based classified output (250 x 250) was not validated as the same spectral library which was used for generating the individual class signatures for classification of the HR image was also used to create the synthetic images. Abundance values from 15% of the pixels obtained from linear unmixing along with the corresponding proportions obtained from the 250 x 250 classified image obtained by MLC were used for training the neurons in MLP. For example, each input sample to the MLP has the abundance values obtained from OSP for each of the four classes (0.2, 0.3, 0.1, 0.4 = 1 or 100 % of a pixel) and the proportion of each class as derived from HR MLC based classified map (0.18, 0.27, 0.2, 0.35 = 1 or 100 % of a pixel) by considering 25 x 25 classified pixels and finding the percentage of each class separately which is equivalent to 1 x 1 LR pixel spatially. Testing was done on the entire output abundance images (100% pixels). |
|
Citation : Uttam Kumar, Kumar Raja. S., Mukhopadhyay. C. and Ramachandra. T.V., 2011. A Multi-layer Perceptron based Non-linear Mixture Model to estimate class abundance from mixed pixels. Proceeding of the 2011 IEEE Students' Technology Symposium 14-16 January, 2011, IIT Kharagpur., pp. 148-153.
|


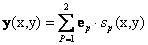 (14)
(14)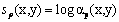 is the contribution of endmember ep and
is the contribution of endmember ep and 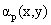 is the fractional abundance of ep at (x,y). A limitation here is that even though all the pixels are mixed in different proportions, there are no instances of pure pixels. If α is 1, we expect the observed hyperspectral signature to be solely from one material, and therefore, ideally it should be identical to the endmember itself. Here, as the abundance increases towards 1, log (α) approaches 0, thereby suppressing the contribution of that particular endmember. On the other hand, if α is 0, log (α) approaches
is the fractional abundance of ep at (x,y). A limitation here is that even though all the pixels are mixed in different proportions, there are no instances of pure pixels. If α is 1, we expect the observed hyperspectral signature to be solely from one material, and therefore, ideally it should be identical to the endmember itself. Here, as the abundance increases towards 1, log (α) approaches 0, thereby suppressing the contribution of that particular endmember. On the other hand, if α is 0, log (α) approaches 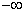 , and therefore, starts dominating in the observed spectral signature. Of course, it will appear as negative numbers. This is against our physical understanding as to how a material which is almost not present in the pixel, contribute to the observation in a dominant way? That is, the model is not able to highlight the endmember of the correct material when its contribution is 1 and gives a wrong endmember when its contribution is 0. To overcome this limitation, we modify the model in (14) by (15):
, and therefore, starts dominating in the observed spectral signature. Of course, it will appear as negative numbers. This is against our physical understanding as to how a material which is almost not present in the pixel, contribute to the observation in a dominant way? That is, the model is not able to highlight the endmember of the correct material when its contribution is 1 and gives a wrong endmember when its contribution is 0. To overcome this limitation, we modify the model in (14) by (15):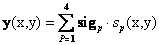 (15)
(15) is the signature corresponding to pth mineral,
is the signature corresponding to pth mineral,  is the contribution of endmember ep and
is the contribution of endmember ep and 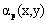 is the fractional abundance of ep in the pixel at (x,y).
is the fractional abundance of ep in the pixel at (x,y).