Introduction

Urban growth modeling is getting more attention as an emerging research area in many disciplines. Urbanisation is a form of metropolitan growth that is a response to often bewildering sets of economic, social, and political forces and to the physical geography of an area. This comes as a result of the recent dramatic increase in urban population that increases the pressure on the infrastructure services. Many cities are now undergoing redevelopment for economic purposes with new roads, infrastructure improvements, etc. This phenomenona is very rapid in India with urban population growing at around 2.3 percent per annum (World Urbanization Prospects, 2005). An increased urban population and growth in urban areas is irreversible with population growth and migration. This dramatic increase in urbanisation has raised the necessity to understand the dynamics of urban growth process for planning of natural resources. It also raises the necessity to understand the dynamics of urban growth process through “growth models” for sustainable distribution of usable resources.

Among the developed growth models, cellular automata (CA), an artificial intelligence technique based urban growth models have better performance in simulating urban development than conventional mathematical models (Batty and Xie, 1994). CA simplifies the simulation of complex systems (Waldrop, 1992). Its aptness in urban modelling is due to the fact that the process of urban spread is entirely local in nature (Clarke and Gaydos, 1998). CA is based on pixels, states, neighbourhood and transition rules, and is being implemented to model the urban growth process due to its ability to fit complex spatial nature using simple and effective rules. Development of CA model involves rule definition and calibration to produce results consistent with historical data, and future prediction with the same rules (Clarke et al., 1997). Many CA-based urban growth models are reported in literatures including the model by White and Engelen (1992; 1993) that involves reduction of space into square grids. They implement the defined transition rules in recursive form to match the spatial pattern. One of the earliest and most well-known models is CA-based “SLEUTH” model that has four major types of data: land cover, slope, transportation, and protected lands (Clarke’s et al., 1997). This is rooted in the work of von Neumann (1966), Hagerstrand (1967), Tobler (1979) and Wolfram (1994). A set of initial conditions in SLEUTH is defined by ‘seed’ cells which are determined by locating and dating the extent of various settlements identified from historical maps, atlases, and other sources. These seed cells represent the initial distribution of urban areas. A set of complex behaviour rules are developed that involves selecting a location randomly, investigating the spatial properties of the neighboring cells, and urbanising the cell based on a set of probabilities.

Despite these achievements in CA urban growth modeling, the selection of CA transition rules remains a research topic. Most of the CA models are usually designed based on individual preference and application requirements with transition rules being defined in an ad hoc manner (Li and Yeh, 2003). Furthermore, most of the developed CA models need intensive computation to select the best parameter values for accurate modeling. This motivates development and implementation of an effective CA-based urban growth model that is easy to calibrate and takes into account the spatial and temporal dynamics of urban growth simultaneously. The objectives of this study are:

1. To develop and implement an effective CA-based urban growth model to simulate the growth as a function of local neighbourhood structure of the input data.

2. To develop a calibration algorithm that takes into consideration spatial and temporal dynamics of urban growth.  

Spatially, the model is calibrated locally to take into account the effect of site specific features while the temporal calibration is set up to adapt the model to the changes over growth pattern with time. Calibration provides the optimal values for the transition rules to achieve accurate urban growth modeling. The input to the urban growth model consists of two types of data:

1. classified images of 1973, 1992 and 2006 where each pixel represents one of the four land use classes – urban, vegetation, water and others.

2. population density maps being represented by pixels in a raster format for the year 1973 and 1992.

CA generates transition rules for each pixel based on the current state of the pixel’s category (in terms of land use class) and population density value of that pixel together, to decide the next state of the pixel after a time epoch, i.e. change in land use from one class to another from 1973 to 1992 and 1992 to 2006. The model is tested for Bangalore city, India by modeling the growth using remote sensing data of various spatial, spectral and temporal resolutions. Later, towards the end of this communication, genetic algorithm (GA) is introduced as a heuristic optimisation technique for selecting optimal model parameters. The possibility of using GA for automatic calibration of the model through proper design of their parameters, including objective function, initial population, selection, crossover and mutation has been explored. Here, a set of strings are used as initial population over which GA runs till convergence. 

The paper is organized as follows: section 2 briefs the study area, followed by data preparation details in section 3 – classification of remote sensing data of three time periods (1973, 1992 and 2006) and generation of population density maps corresponding to the year 1973 and 1992. Section 4 introduces CA; section 5 presents the simulated results from the CA model; section 6 deals with implementation of GA to model urban growth; section 7 discusses the results of modeling the urbanisation process and its relation to public policy followed by concluding remarks in section 8.

Study Area

Bangalore city is the principal administrative, cultural, commercial, industrial, and knowledge capital of the state of Karnataka. The administrative jurisdiction was widened in 2006 by merging the existing area of Bangalore city spatial limits with 8 neighbouring Urban Local Bodies (ULBs) and 111 Villages of Bangalore Urban District to form Greater Bangalore. Bangalore has spatially grown more than ten times since 1949 from 69 square kilometers to 741 square kilometers in 2006. Now, Bangalore (figure 1) is the fifth largest metropolis in India currently with a population of about 7 million (Ramachandra and Kumar, 2008).

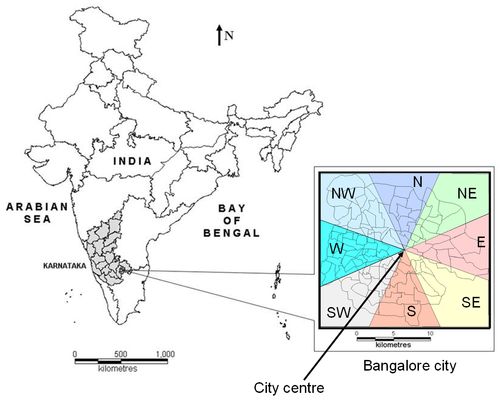
Figure 1: Study Area: Bangalore city, Greater Bangalore

Bangalore city is composed of 100 wards. For our analysis, the city was divided into 8 zones [North (N), Northeast (NE), East (E), Southeast (SE), South (S), Southwest (SW), West (W), and Northwest (NW)] with their origin from the ‘city centre’ as shown in figure 1.