HYBRID MIXTURE MODEL (HMM)

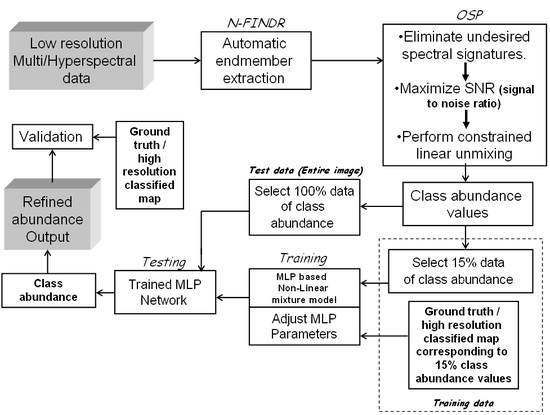
Despite many attempts of using ANN for unmixing models, ANN-based non-linear unmixing techniques remain largely unexplored for general-purpose applications [12]. Only [1,7,9,29] have produced some of the pioneering work in NLMM to be considered as a general model for ANN-based non-linear unmixing independent of physical properties of the observed classes. Some of these applications are, however, difficult and complex in their implementation. LMM is easy to implement, generalize and reconstruct. Therefore, in our approach, we make use of the LMM output as the input to NLMM to refine the fraction estimates. The MLP architecture can be extended to produce a continuous-values output for sub-pixel classification problems. The entries to the MLP model is the abundance ai (see Figure 1) output obtained from LMM, which is denoted by aⁱLMM where i = 1, …, E, and the neuron count at the input layer equals the number of endmember classes (estimated by a fully constrained LMM) as shown in Figure 2[30].

Figure 1. Architecture of the multi-layer perceptron (MLP) model

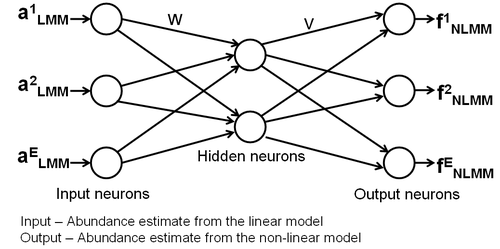
Figure 2. Hybrid mixture model(HMM) method for spectral mixture analysis

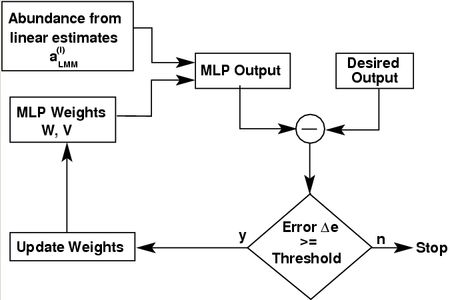
The training process is based on an error back-propagation algorithm [29], where the respective weights in the output and hidden nodes (W and V in Figure 3) are modified depending on the error (δe), the input data and the learning parameter alpha (α). The activation rule used here for the hidden and output layer nodes is defined by the logistic function

δe of the output layer is calculated as the difference between the fraction (f) estimation outputs fⁱNLMM, i = 1, … E, provided by the network architecture and a set of desired outputs given by actual fractional abundances available for the training samples. The resulting error is back-propagated until the convergence is reached. One of the earlier works by Plaza et al. [12] attempted a similar NLMM methodology, which made use of a modified MLP neural network (NN), whose entries were determined by a linear activation function provided by a Hopfield NN (HNN). The combined HNN/MLP method used the LMM to provide an initial abundance estimation and then refined the estimation using a non-linear model. As per Plaza et al. [12], this was the first and only approach in the literature that integrated linear and NLMM.

Figure 3. MLP structural diagram