IMAGE FUSION TECHNIQUES

Images are radiometrically and geometrically corrected (at pixel level) and geo-registered considering the topographic undulations. For all methods discussed here (except generalised Laplacian pyramid), it is assumed that LSR MS images are upsampled to the size of HSR PAN image.

Component Substitution (COS) – A set of LSR M-bands MS data (MS_LOW) and a HSR PAN data (PAN_HIGH) fusion using COS method involves three steps:

• Transforming the MS data from spectral space to some other feature space by linear transformations.
• Substituting one component with the HSR data derived from PAN.
• Transforming the transformed band back to the spectral space to get HSR MS data. The fused MS image is given by:

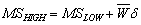                             (1)

where,  is the fused image, 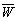 is the modulation coefficient,  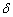is the spatial detail of redundant information I, 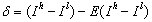, , 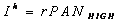 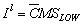and 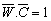.  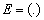is the expectation of 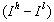. First, a linear regression of MS and PAN sensor SRF (spectral response function) is carried out. The regression coefficient  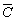is obtained for each MS band. Next, the area of the part covered by both (intersection) of PAN SRF (denoted by 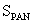) and SRF of all the pooled MS bands (denoted as 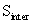) are calculated. Ratio of  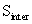and 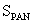 is calculated (denoted by r), for IKONOS. W is calculated by

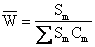                                  (2)

where 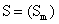 is the area of the part covered by both (union) SRF of MS band m and PAN, and  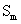implies how much information is recorded by both the MS band m while it is recorded by PAN sensor [2].

Local Mean and Variance Matching (LMVM) – LMVM matches both the local mean and variance values of the PAN image with those of the original LSR spectral channel given by

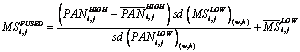                               (3)

where, 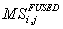 is the fused image,  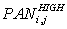and 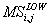 are respectively, the HSR and LSR images at pixel coordinates i, j, 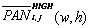,  are local means calculated inside the window of size (w, h), sd is the local standard deviation, and 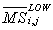 is the mean of the LSR image [3].

Modified IHS (Intensity Hue Saturation) – Here the input intensity (PAN band) is modified so that it looks more like the intensity of the input MS bands. The steps are:

1. Choose the β coefficients: β coefficients represent the relative contributions of each portion of the electromagnetic spectrum to the PAN band. A regression analysis is performed on M bands vs. the PAN band. If the MS and PAN data come from the same sensor, a linear regression is sufficient to derive a good relationship between the two datasets otherwise it may be possible to improve by using higher-order terms.

2. Choose the α coefficients: The desired output is equally weighted toward Red (R), Green (G), and Blue (B). In such cases, the α coefficients are equal and given by 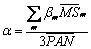     _..                 (4)

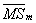   =average of band m; 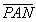=average of PAN band; 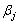=coefficient for band m.

3. Generate modulation ratio: Apply an RGB-to-IHS transform on the three MS bands and generate intensity modification ratio (r₁),
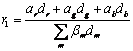                        (5)

   where, a_r= numerator coefficient for red DN value, d_r= DN value of band used for red output, a_g= numerator coefficient for green DN value, d_g= DN value of band used for green output, ab= numerator coefficient for blue DN value, d_b= DN value of band used for blue output, β_m= denominator coefficient for DN value of band m and d_m= DN value of band m.

4. Reverse transformation: Multiply the modification ratio r₁ by the PAN band. Transform the modified IHS data back to RGB space to generate the final product using the modified intensity [4].

Fast Fourier Transformed-enhanced IHS (FFT-IHS) – The basic idea is to modify the input HSR PAN image so that it looks more like the intensity component of the input MS image. Instead of using the total replacement of the intensity component, this method uses a partial replacement based on FFT filtering [5].

1. Transform the MS image from RGB to IHS colour space to obtain the IHS components.
2. Low Pass (LP) filter the intensity component (I) in the Fourier domain.
3. High Pass (HP) filter the PAN image in Fourier domain.
4. Add the high frequency filtered PAN image to the low frequency filtered intensity component, I´.
5. Match I´ to the original I to obtain a new intensity component, I´´.
6. Perform an IHS to RGB transformation on I´´, together with original H and S components to create the fused images.

Generalised Laplacian Pyramid (GLP) – The method is a generalisation of the Laplacian pyramid for rational ratio [6]. Two functions are used: the function “reduce” reduces the size of an image of a given q ratio; the function “expand” increases the size of an image of a given p ratio. Degrade an image with a ratio p/q > 1 (“reduce p/q”) is done by “expand” by q and “reduce” by p. Interpolate an image can be performed by “expand” by p then “reduce” by q (“expand p/q”). The fusion process is done as follows on each MS image. PAN is decomposed through generalized Laplacian pyramid. The two first levels of Laplacian images are calculated:

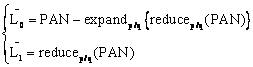                                   (6)

The MS image is interpolated into MSUPGRADE by “expand” by p and “reduce” by q. A coefficient w is calculated from each MS band and 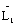,  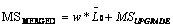with 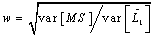, where var is the variance calculated for each MS band separately.

 Local Regression (LR) – The rationale for using a local modelling approach [7] is based on the fact that edges are manifestations of object or material boundaries that occur wherever there is a change in material type, illumination, or topography. The geometrically co-registered PAN band is blurred to match the equivalent resolution of the MS image. A regression analysis within a small moving window (5 x 5) is applied to determine the optimal local modelling coefficients and the residual errors for the pixel neighbourhood using a single MS and the degraded PAN band. Thus,

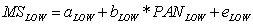                    (7)

where, 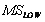 is the LSR MS image,  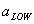and 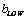 are the coefficients,  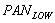is the degraded LSR PAN band,  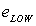is the residual derived from the local regression analysis. Fused image (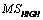) is given by:

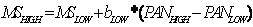                     (8)

Smoothing Filter (SF) – It is given by: 

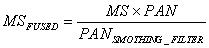                     (9)

MS is a pixel of LSR image co-registered to HSR PAN band, 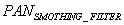 is average filtered PAN image over a neighbourhood equivalent to the actual resolution of MS image. SF [8] is not applicable for fusing images with different illumination and imaging geometry, such as TM and ESR-1 SAR.

Sparkle – Sparkle is a proprietary algorithm developed by the Environmental Research Institute of Michigan (ERIM) [9]. Sparkle treats the digital value of a pixel as being the sum of a low-frequency component and a high-frequency component. It assumes that the low-frequency component is already contained within the MS data and performs two sub-tasks: (1) separate the sharpening image into its low- and high-frequency components, and (2) transfer the high-frequency component to the MS image. The high-frequency component of an area is transferred by multiplying the MS values by the ratio of total sharpening value to its low-frequency component as given by equation 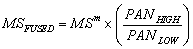(10):

                     (10)

where, 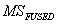=fused HSR MS image, 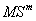=LSR MS mth band, 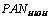=HSR PAN image, 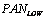= 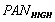* h0, h0 is a LP filter (average or smoothing filter).

 SVHC – SVHC (Simulateur de la Vision Humaine des Couleurs) is proposed by CNES, Toulouse France by Marie-Jose Lefevre-Fonollosa [6]. The algorithm is as follows:

1. Perform a RGB to IHS transformation ( 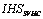from three MS channels).
2. Keep H and S images.
3. Create a low-frequency resolution PAN image (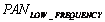), by the suppression of high spatial frequency.
4. Compute ratio (r), .
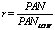5. Compute .
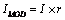6. Inverse transform from IMODHS to .

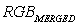Synthetic Variable Ration (SVR) – It is given by 

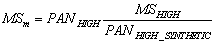                (11)

where, 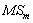 is the grey value of the mth band of the merged HSR IKONOS image,  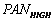is the grey value of the original IKONOS PAN image,  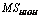is the grey value of mth band of IKONOS MS image modified to have the DN as the original IKONOS PAN image,  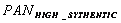is the grey value of the HSR synthetic PAN image simulated through 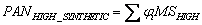.  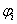were calculated directly through multiple regression of the original PAN image and the original MS bands (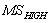) which are used in merging and have the same pixel size as  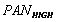[10].