MODEL

Smoothing Filter-based Intensity Modulation (SFIM) is a general spectral preserve image fusion technique applicable to co-registered multi resolution images (Liu, 2000, Bharath, 2009). SFIM is based on a simplified solar radiation and land surface reflection model (equation 1). Spatial details can be modulated to a co-registered LR MSS band without altering its spectral properties and contrast by using a ratio between a HR image and its low pass (smoothing filter) filtered image.

Digital Number (DN) of an optical image in the reflective spectral band (λ) is dependent on irradiance E(λ) and the spectral reflectance of the land surface ρ(λ), is given by

Similarly DN value in a LR image of spectral band λ is represented by DN(λ)_low and DN value of the corresponding pixel in a HR image of spectral band γ is given by DN(γ)_high. If the two images are taken in similar solar illumination conditions, then

SFIM is given by,

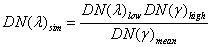(4)

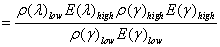(5)

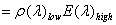(6)

where DN(λ)_simis the simulated HR pixel corresponding to DN(λ)_lowand DN(γ)_mean is the local mean of DN(γ)_high over a neighbourhood equivalent to the resolution of DN(λ)_low. For a given solar radiation, irradiance upon a land surface is controlled by topography. If the two images are quantified to the same DN range, we can presume E(λ) ≈ E(γ) for any given resolution because both vary with topography in the same way (Liu et al., 1997). We can also presume ρ(λ)_low ≈ ρ(γ)_high if there is no significant spectral variation within the neighbourhood for calculating DN(γ)mean. Thus in

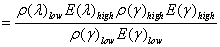(7)

E(λ)_low and E(γ)_low cancel each other; ρ(γ)_low and ρ(γ)_high also cancel each other; and E(γ)_high can be replaced by E(λ)_high. We then have a final simple solution of (6). The local mean DN(γ)_mean is calculated for every pixel of the HR image using a smoothing convolution filter. DN(γ)_mean is considered as a simulated LR pixel derived from the HR image pixels by spatial smoothing. The image of DN(γ)_mean is equivalent to the image of DN(λ)_low in topography and texture because they both have a pixel size of the higher resolution image, and a spatial resolution of the lower resolution image. The final result, the image of DN(λ)_sim, is a product of the topography and texture of higher resolution, E(λ)_high, introduced from the higher resolution image, and the lower resolution spectral reflectance of the original lower image, ρ(γ)_low. It is therefore independent of the spectral property of the HR image used for intensity modulation. As the spectral difference between the lower and the higher resolution images is not fundamental to the operations, equation 6 can be rewritten as:

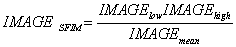(8)

where IMAGE_low is a pixel of a LR image co-registered to a HR image of IMAGE_high, IMAGE_mean is a smoothed pixel of IMAGE_high using averaging filter over a neighbourhood equivalent to the actual resolution of IMAGE_low. The ratio between IMAGE_high and IMAGE_mean in equation (8) cancels the spectral and topographical contrast of the HR image and retains the higher resolution edges only. SFIM is therefore reliable to the spectral properties as well as contrast of the original lower resolution image. However, for SFIM operations, the lower resolution image must be interpolated to the same pixel size as the higher resolution image by the co-registration process. Also, IMAGE_low must have the same pixel size as IMAGE_high though with a lower resolution. Otherwise, the spatial information of HR image cannot be fully integrated into the LR image.