|
DERIVATION OF LAND SURFACE TEMPERATURE (LST)
LST from Landsat TM: The TIR band 6 of Landsat-5 TM was used to calculate the surface temperature of the area. The digital number (DN) was first converted into radiance LTM using (Artis and Carnhan, 1982; Ramachandra and Kumar, 2009):
LTM = 0.124 + 0.00563 * DN ….. (Equation 1)
The radiance was converted to equivalent blackbody temperature TTMSurface at the satellite using
TTMSurface = K2/(K1 – lnLTM) – 273 ….. (Equation 2)
The coefficients K1 and K2 depend on the range of blackbody temperatures. In the blackbody temperature range 260-300K the default values (Singh, S. M., 1988) for Landsat TM are K1 = 4.127 and K2 = 1274.7. Brightness temperature is the temperature that a blackbody would obtain in order to produce the same radiance at the same wavelength (λ = 11.5 μm). Therefore, additional correction for spectral emissivity (ε) is required to account for the non-uniform emissivity of the land surface. Spectral emissivity for all objects are very close to 1, yet for more accurate temperature derivation emissivity of each LC class is considered separately. Emissivity correction is carried out using surface emissivity for the specified LC (table 1) derived from the methodology described in Snyder et al., (1998) and Stathopoulou et al. (2006).
Table 1: Surface emissivity values by LC type
| LC type |
Emissivity |
| Densely urban |
0.946 |
| Mixed urban (Medium Built) |
0.964 |
| Vegetation |
0.985 |
| Water body |
0.990 |
| Others |
0.950 |
The procedure involves combining surface emissivity maps obtained from the Normalized Difference Vegetation Index Thresholds Method (NDVITHM) (Sobrino and Raissouni, 2000) with LC information. The emmissivity corrected land surface temperature (Ts) were finally computed as follows (Artis and Carnhan, 1982)
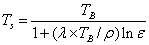 ….. (Equation 3) ….. (Equation 3)
where, λ is the wavelength of emitted radiance for which the peak response and the average of the limiting wavelengths (λ = 11.5 μm) were used, ρ = h x c/σ (1.438 x 10-2 mK), σ = Stefan Bolzmann’s constant (5.67 x 10-8 Wm-2K-4 = 1.38 x 10-23 J/K), h = Planck’s constant (6.626 x 10-34 Jsec), c = velocity of light (2.998 x 108 m/sec), and ε is spectral emissivity.
LST from Landsat ETM+: The TIR image (band 6) was converted to a surface temperature map according to the following procedure (Weng et al., 2004). The DN of Landsat ETM+ was first converted into spectral radiance LETM using equation 4, and then converted to at-satellite brightness temperature (i.e., black body temperature, TETMSurface), under the assumption of uniform emissivity (ε ≈ 1) using equation 5 (Landsat Project Science Office, 2002):
LETM = 0.0370588 x DN + 3.2 ….. (Equation 4)
TETMSurface = K2/ln (K1/ LETM + 1) ….. (Equation 5)
where, TETMSurface is the effective at-satellite temperature in Kelvin, LETM is spectral radiance in watts/(meters squared x ster x μm); and K2 and K2 are pre-launch calibration constants. For Landsat-7 ETM+, K2 = 1282.71 K and K1 = 666.09 mWcm-2sr-1μm-1 were used (http://ltpwww.gsfc.nasa.gov/IAS/handbook/handbook_htmls/chapter11/chapter11. html). The emissivity corrected land surface temperatures Ts were finally computed by equation 3.
|


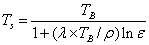 ….. (Equation 3)
….. (Equation 3)