Methods
Urban dynamics was analysed using temporal remote sensing
data of the period 1973e2010. The time series spatial data acquired
from Landsat Series Multispectral sensor (57.5 m) and Thematic
mapper (28.5 m) sensors for the period 1973e2010 were downloaded
from public domain (http://glcf.umiacs.umd.edu/data).
Survey of India (SOI) topo-sheets of 1:50,000 and 1:250,000 scales
were used to generate base layers of city boundary, etc. The process
of the analysis is threefold as described in Fig. 3, which includes preprocessing, analysis of land cover and land use, finally gradient
wise zonal analysis of Delhi.
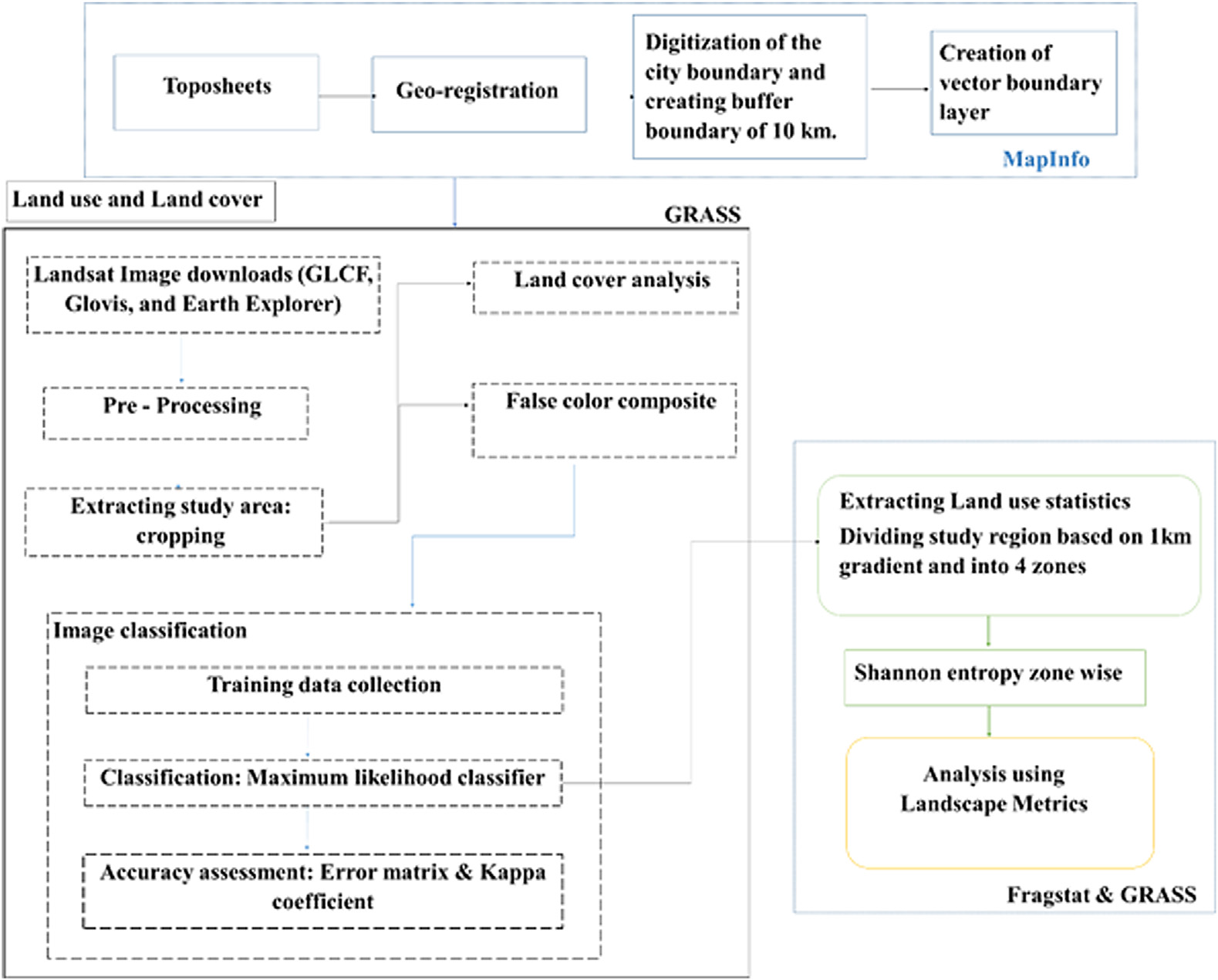
Fig. 3. Procedure adopted for classifying the landscape and computation of metrics.
-
Preprocessing: Remote sensing data (Landsat series) for Delhi
acquired for different time period were downloaded from
Global Land Cover Facility (http://www.glcf.umd.edu/index.
shtml) and (http://www.landcover.org/), United States Geological
Survey (USGS) Earth Explorer (http://edcsns17.cr.usgs.gov/
NewEarthExplorer/) and Glovis (http://www.glovis.usgs.gov).
The remote sensing data obtained were geo-referenced, geocorrected,
rectified and cropped pertaining to the study area.
Geo-registration of remote sensing data (Landsat data) has been
done using ground control points collected from the field using
pre calibrated GPS (Global Positioning System) and also from
known points (such as road intersections, etc.) collected from
geo-referenced topographic maps published by the Survey of
India. The Landsat satellite data of 1973 (with spatial resolution
of 57.5 m 57.5 m (nominal resolution) and 1989e2010
(28.5m 28.5m(nominal resolution)) were resampled to 30m
in order to maintain uniformity in spatial resolution across
different time period. The study area includes the Delhi
administrative area with 10 km buffer.
-
Land Cover analysis: Land Cover analysis was performed to
understand the changes in the vegetation cover during the
study period in the study region. Normalised difference vegetation
index (NDVI) was found suitable and was used for
measuring vegetation cover. NDVI values ranges from values 1
to þ1. Very low values of NDVI (0.1 and below) correspond to
soil or barren areas of rock, sand, or urban builtup. Zero indicates
the water cover. Moderate values represent low density
vegetation (0.1e0.3), while high values indicate thick canopy
vegetation (0.6e0.8)..
-
Land use analysis: The method involves i) generation of False Colour Composite (FCC) of remote sensing data (bands – green, red and NIR). This helped in locating heterogeneous patches in the landscape ii) selection of training polygons (these correspond to heterogeneous patches in FCC) covering 15% of the study area and uniformly distributed over the entire study area, iii) loading these training polygons co-ordinates into pre-calibrated GPS, vi) collection of the corresponding attribute data (land use types) for these polygons from the field. GPS helped in locating respective training polygons in the field, iv) supplementing this information with Google Earth v) 60% of the training data has been used for classification, while the balance is used for validation or accuracy assessment.
Land use analysis was carried out using supervised pattern classifier - Gaussian maximum likelihood algorithm. Remote sensing data was classified using signatures from training sites that include all the land use types detailed in table 3. Mean and covariance matrix are computed using estimate of maximum likelihood estimator. This technique is proved superior classifier as it uses various classification decisions using probability and cost functions (Duda et al., 2000, Ramachandra et al., 2012b).
Maximum Likelihood classifier is then used to classify the data using these signatures generated. This method is considered as one of the superior methods as it uses various classification decisions using probability and cost functions (Duda et al., 2000). Mean and covariance matrix are computed using estimate of maximum likelihood estimator. Land Use was computed using the temporal data through open source program GRASS - Geographic Resource Analysis Support System (http://ces.iisc.ac.in/foss). Signatures were collected from field visit and help of Google earth. 60% of the total generated signatures were used in classification, 40% signatures were used in validation and accuracy assessment. Classes of the resulting image were reclassed and recoded to form four land-use classes. The excessive noise in the classified images was removed by moving 3 X 3 median filter on it.
Land use Class |
Land uses included in the class |
Urban |
This category includes residential area, industrial area, and all paved surfaces and mixed pixels having built up area. |
Water bodies |
Tanks, Lakes, Reservoirs. |
Vegetation |
Forest, Cropland, nurseries. |
Others |
Rocks, quarry pits, open ground at building sites, kaccha roads. |
Table 3: Land use classification categories
-
Accuracy assessment: These methods evaluate the performance of classifiers (Mitrakis et al., 2008). This is done either through comparison of kappa coefficients (Congalton et al., 1983). For the purpose of accuracy assessment, a confusion matrix was calculated. Accuracy assesment, Kappa coefficient, are common measurements used in various publications to demonstrate the effectiveness of the classifications (Congalton, 1991; Lillesand & Kiefer, 2005). Recent remote sensing data (2010) was classified using the collected training samples. Statistical assessment of classifier performance based on the performance of spectral classification considering reference pixels is done which include computation of kappa (κ) statistics and overall (producer's and user's) accuracies. For earlier time data, training polygon along with attribute details were compiled from the historical published topographic maps, vegetation maps, revenue maps, etc.
-
Zonal analysis: City boundary along with the buffer region has
been divided into 4 zones: North east, Southwest, Northwest,
South east for further analysis as the urbanization is not uniform
in all directions. As most of the definitions of a city or its growth
is defined in directions it was considered more appropriate to
divide the regions in 4 zones based on direction. Zones were
divided considering the Central pixel (Central Business district).
The growth of the urban areas along with the agents of changes
is understood in each zone separately through the computation
of urban density for different periods.
-
Division of these zones to concentric circles (Gradient Analysis):
Each zone was divided into concentric circle of incrementing
radius of 1 km radius from the center of the city, this analysis
helped in visualising the process of change at local level and to
understand the agents responsible for changes. This helps in
identifying the causal factors and locations experiencing various
levels (sprawl, compact growth, etc.) of urbanization in response
to the economic, social and political forces. This approach
(zones, concentric circles) also helps in visualizing the forms of
urban sprawl (low density, ribbon, leaf-frog development). The
built up density in each circle is monitored overtime using time
series analysis. This helps the city administration in understanding
the urbanization dynamics to provide appropriate
infrastructure and basic amenities.
-
Shannon’s entropy: Further to understand the growth of the
urban area in specific zone and to understand if the urban area is
compact or divergent the Shannon’s entropy (Sudhira et al.,
2004; Ramachandra et al., 2012a,b) was computed for each
zones. Shannon’s entropy (Hn) given in Eq. (1), explains clearly
the development process and its characteristics.
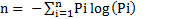 …..(1) …..(1)
Where Pi is the proportion of the built-up in the ith concentric circle. As per Shannon’s Entropy, if the distribution is maximally concentrated in one circle the lowest value zero will be obtained. Conversely, if it is an even distribution among the concentric circles will be given maximum of log n.
- Computation of spatial metrics: Spatial metrics are helpful to quantify spatial characteristics of the landscape. Selected spatial metrics were used to anlayse and understand the urban dynamics, FRAGSTATS (McGarigal and Marks in 1995) was used to compute metrics at three levels: patch level, class level and landscape level. Annexure I(a-d). below gives the list of the metrics along with their description considered for the study.
Area metrics: Area metrics quantifies the composition of the landscape and provides information about the area occupied by various patches in the landscape. Annexure Ia provides description of area metrics.
Shape Metrics: Shape metrics listed in Annexure Ib quantify the landscape configuration by measuring shape complexity of patches at patch, class and landscape level. Shape is a difficult parameter to quantify concisely in a metric (McGarigal and Marks, 1994). All the shape indices are based on perimeter to area ratio and thus they help in interpreting irregularities in urban patches.
Edge/Border Metrics: Edge metrics (Annexure Ic) quantify length and distribution of the amount of edge between patches (Frohn and Hao, 2006). They represent landscape configuration, even though they are not spatially explicit at all (McGarigal and Marks, 1995).These edge attributes can provide critical information for quantifying and understanding urban and landscape fragmentation.
Compactness Metrics/Contagion and Interspersion Metrics: Compaction is the formation of rounded patches in a circular shape that makes them more compact (Aguilera et al., 2011). These metrics liosted in Annexure Id quantify landscape configuration. Compactness Metrics is the measure of individual patch shape and fragmentation of overall landscape.
Citation : T.V. Ramachandra, Bharath H. Aithal and M.V. Sowmyashree, 2015. Monitoring urbanization and its implications in a mega city from space: Spatiotemporal patterns and its indicators, Journal of Environmental Management, 148 (2015):67-81, http://dx.doi.org/10.1016/j.jenvman.2014.02.015.
Corresponding author:
|
| |
Dr. T.V. Ramachandra
Energy & Wetlands Research Group, CES TE 15
Centre for Ecological Sciences
New Bioscience Building, Third Floor, E –Wing
[Near D-Gate], Indian Institute of Science,
Bangalore – 560 012, INDIA.
|
Tel : +91-80-2293 3099/2293 3503 - extn 107
Fax : 91-80-23601428 / 23600085 / 23600683 [CES-TVR]
E-mail : cestvr@ces.iisc.ac.in, energy@ces.iisc.ac.in,
Web : http://wgbis.ces.iisc.ac.in/energy |
|


