Uttam Kumar | S. Kumar Raja | C. Mukhopadhyay | T. V. Ramachandra* |
| Citation: Uttam Kumar, S. Kumar Raja, C. Mukhopadhyay and T. V. Ramachandra , 2011, Hybrid Bayesian Classifier for Improved Classification Accuracy. IEEE Geoscience and Remote Sensing letters, Vol. 8, No. 3, pp. 473 – 476. | |||
|
REVIEW OF METHODS Linear Unmixing: With K spectral bands and M classes (C1,..,CM), each pixel has an associated K-dimensional pixel vector
where,
which is used to project
After maximizing the SNR, an optimal estimate of
Note that Bayesian classifier: Associated with any pixel, there is an observation
In (6), since
|
*T. V. Ramachandra, Senior Member, IEEE, is with the Centre for Ecological Sciences, Centre for Sustainable Technologies and Centre for Infrastructure, Sustainable Transport and Urban Planning, Indian Institute of Science (IISc), Bangalore, India. Uttam Kumar, Student Member, IEEE, is with the Department of Management Studies and Centre for Sustainable Technologies, Indian Institute of Science, India. (e-mail: uttam@ces.iisc.ac.in). Chiranjit Mukhopadhyay is with the Department of Management Studies, Indian Institute of Science, Bangalore, India (e-mail: cm@mgmt.iisc.ac.in). S. Kumar Raja is with the VISTA Group, IRISA, Rennes, France and Thomson R&D France, SNC Cesson - Sévigné, France (email: s.kumar.raja@yahoo.com). |


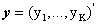 whose components are the gray values corresponding to the K spectral bands. Let
whose components are the gray values corresponding to the K spectral bands. Let 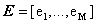 , where, for
, where, for 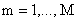 ,
, 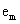 is a
is a 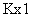 column vector representing the endmember spectral signature of the mth target material. For a pixel, let
column vector representing the endmember spectral signature of the mth target material. For a pixel, let 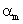 denote the fraction of the mth target material signature, and
denote the fraction of the mth target material signature, and 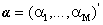 denote the M-dimensional abundance column vector. The linear mixture model for
denote the M-dimensional abundance column vector. The linear mixture model for 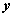 is given by
is given by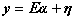 (1)
(1)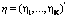 , are i.i.d.
, are i.i.d. 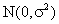 [
[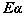 is a desired signal vector to be detected. Since, OSP detects one signal (target) at a time, we divide a set of M targets into desired
is a desired signal vector to be detected. Since, OSP detects one signal (target) at a time, we divide a set of M targets into desired 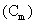 and undesired
and undesired 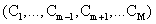 targets. A logical approach is to eliminate the effects of undesired targets that are considered as “interferers” to
targets. A logical approach is to eliminate the effects of undesired targets that are considered as “interferers” to 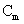 before the detection of
before the detection of 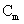 takes place. Now, in order to find
takes place. Now, in order to find 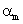 , the desired target material is
, the desired target material is 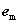 . The term
. The term 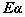 in (1) can be rewritten to separate the desired spectral signature
in (1) can be rewritten to separate the desired spectral signature 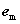 :
: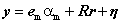 (2)
(2) 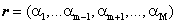 and
and 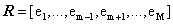 . Thus the interfering signatures in
. Thus the interfering signatures in 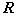 can be removed by the operator,
can be removed by the operator,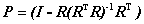 (3)
(3) into a space orthogonal to the space spanned by the interfering spectral signatures, where
into a space orthogonal to the space spanned by the interfering spectral signatures, where  is the
is the  identity matrix [
identity matrix [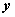 with
with 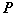 , and noting that
, and noting that 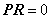 ,
,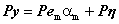 . (4)
. (4)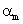 is
is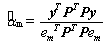 (5)
(5)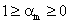 and thus
and thus 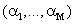 can be taken as proportional probabilities of the M classes i.e.
can be taken as proportional probabilities of the M classes i.e. 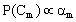 .
.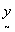 . With M classes
. With M classes 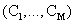 , Bayesian classifier calculates the posterior probability of each class conditioned on
, Bayesian classifier calculates the posterior probability of each class conditioned on 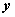 [
[ (6)
(6)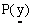 is constant for all classes, only
is constant for all classes, only 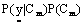 is considered.
is considered. 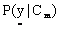 is computed assuming class conditional independence, so,
is computed assuming class conditional independence, so, 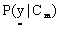 is given by
is given by (7)
(7)