1Energy Research Group, Center for Ecological Sciences; Department of Management Studies; & Centre for Sustainable Technologies, Indian Institute of Science, Bangalore, India
2Department of Management Studies, Indian Institute of Science, Bangalore, India,
3Energy Research Group, Centre for Ecological Sciences; Centre for Sustainable Technologies; & Centre for Infrastructure, Sustainable Transport and Urban Planning (CiSTUP), Indian Institute of Science, Bangalore, India, Email: cestvr@ces.iisc.ac.in
Citation: Uttam Kumar, Mukhopahyay C and Ramachandra T V, 2015. Multi resolution spatial data mining for assessing land use patterns, Chapter 4, In Data mining and warehousing, Sudeep Elayidom (Eds), CENGAGE Learning, India Pvt Ltd., Pp 97-138.
Hybrid Bayesian Classifier (HBC)
HBCis based on linear unmixing and Bayesian classifier, to assign a class label to each pixel in a high spatial-low spectral resolution (HS-LSR) MS data (Kumar et al., 2011). The prior probabilities of the different classes in the Bayesian classifier to classify each pixel in the HS-LSR data such as IRS LISS-III MS and IKONOS MS are obtained from abundance estimates by unmixing low spatial-high spectral resolution (LS-HSR) MS data such as MODIS and Landsat ETM+ respectively. The terms HS-LSR and LS-HSR are relative, depending upon the spatial resolution of the images. For example, MODIS bands are referred as LS-HSR and IRS LISS-III MS bands are HS-LSR data, while Landsat ETM+ bands are LS-HSR and IKONOS MS bands are HS-LSR data. The reason for selecting MODIS and Landsat ETM+ images as LS-HSR supplement data is because of their economic viability and high temporal frequency that enables their procurement for any part of the globe, throughout the year corresponding to any HS-LSR data. However, the technique in general, can be applied on any other LS-HSR (such as hyperspectral bands) and HS-LSR (such as multispectral bands) data classification. The novelty of this approach lies in the fact that low spatial-high spectral and low spectral-high spatial resolution MS data are combined to improve the classification results which can be thought of as a fusion process, in the sense, that information from two different sources (sensors) are combined to arrive at an improved classified image by systematically exploiting the relevant information from both the sources as shown in figure 11.
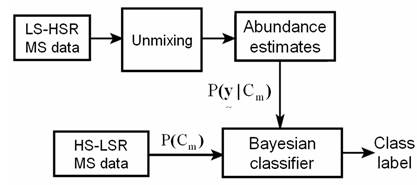
Figure 11: Hybrid Bayesian Classifier.
In the following section, linear unmixing using Orthogonal Subspace Projection (OSP) and Bayesian classifier are discussed. Next, HBC is discussed with experimental results and validation.
6.1 Linear unmixing: With M spectral bands and N classes (C1,..,CN), each pixel has an associated M-dimensional pixel vector  whose components are the pixel intensities corresponding to the M spectral bands. Let whose components are the pixel intensities corresponding to the M spectral bands. Let 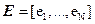 , where, for , where, for 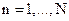 , ,  is a is a 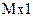 column vector representing the endmember spectral signature of the nth target material. For a pixel, let column vector representing the endmember spectral signature of the nth target material. For a pixel, let  denote the fraction of the nth target material signature, and denote the fraction of the nth target material signature, and  denote the N-dimensional abundance column vector. The linear mixture model for denote the N-dimensional abundance column vector. The linear mixture model for  is given by is given by
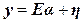 (21) (21)
where, 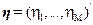 , are i.i.d. , are i.i.d. 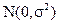 (Kumar et al., 2008). Equation (19) represents a standard signal detection model where (Kumar et al., 2008). Equation (19) represents a standard signal detection model where 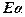 is a desired signal vector to be detected. Since, OSP detects one target at a time, we divide a set of N targets into desired is a desired signal vector to be detected. Since, OSP detects one target at a time, we divide a set of N targets into desired  and undesired and undesired 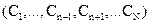 targets. A logical approach is to eliminate the effects of undesired targets that are considered as “impeders” to targets. A logical approach is to eliminate the effects of undesired targets that are considered as “impeders” to 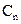 before detecting before detecting . To estimate . To estimate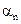 , the desired target material is , the desired target material is  . The term . The term  in (21) can be rewritten to separate the desired spectral signature in (21) can be rewritten to separate the desired spectral signature 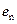 : :
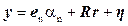 (22) (22)
where 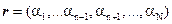 and and 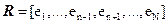 . Thus the interfering signatures in . Thus the interfering signatures in  can be removed by the operator, can be removed by the operator,
 (23) (23)
which is used to project 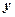 into a space orthogonal to the space spanned by the interfering spectral signatures, where into a space orthogonal to the space spanned by the interfering spectral signatures, where 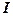 is the is the  identity matrix (Change, 2005). Operating on identity matrix (Change, 2005). Operating on  with with  , and noting that , and noting that 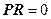 , ,
 . (24) . (24)
After maximizing the SNR, an optimal estimate of 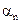 is is
 (25) (25)
Note that  and thus and thus 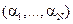 can be taken as proportional probabilities of the N classes i.e. can be taken as proportional probabilities of the N classes i.e. 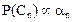 . .
6.2 Bayesian classifier: Associated with any pixel, there is an observation 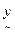 . With N classes . With N classes 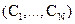 , Bayesian classifier calculates the posterior probability of each class conditioned on , Bayesian classifier calculates the posterior probability of each class conditioned on  (Han and Kamber): (Han and Kamber):
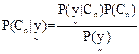 (26) (26)
In (26), since 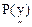 is constant for all classes, only is constant for all classes, only 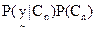 is considered. is considered. 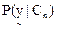 is computed assuming class conditional independence, so, is computed assuming class conditional independence, so,  is given by is given by 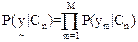 (27) (27)
- Hybrid Bayesian Classifier (HBC):HBC uses the abundance of each class obtained from LS-HSR data by linear unmixing as prior probability while classifying the HS-LSR data using Bayesian classifier of the same geographical area and time frame. That is, given the observation vector
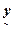 for a pixel, it is classified to fall in class l if for a pixel, it is classified to fall in class l if 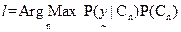 , where , where  is as in (27) calculated using the HS-LSR data and is as in (27) calculated using the HS-LSR data and 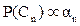 calculated using the LS-HSR data. The assumptions are: (i) if there are r HS-LSR pixels contained in one LS-HSR pixel, i.e. resolution ratio is (r:1), the prior probabilities for all the r HS-LSR pixels are equal corresponding to the same LS-HSR pixel, and (ii) the two data types have a common origin or upper left corner, i.e. the edges of the r x r HS-LSR pixels overlaps exactly with the corresponding LS-HSR pixel. The limitations are: (i) (K-1) should be ≥ M in LS-HSR data and (ii) M in HS-LSR should be ≤ M in LS-HSR data. calculated using the LS-HSR data. The assumptions are: (i) if there are r HS-LSR pixels contained in one LS-HSR pixel, i.e. resolution ratio is (r:1), the prior probabilities for all the r HS-LSR pixels are equal corresponding to the same LS-HSR pixel, and (ii) the two data types have a common origin or upper left corner, i.e. the edges of the r x r HS-LSR pixels overlaps exactly with the corresponding LS-HSR pixel. The limitations are: (i) (K-1) should be ≥ M in LS-HSR data and (ii) M in HS-LSR should be ≤ M in LS-HSR data.
- Experimental Results:Two separate experiments were carried out. In the first experiment, LISS-III MS data (3 bands of 23.5m x 23.5m spatial resolution resampled to 25m, acquired on December 25, 2002) of 5320 x 5460 size and MODIS 8-day composite data (7 bands of 250m x 250m, acquired from 19-26 December, 2002) of 532 x 546 dimension were co-registered with known ground control points (RMSE - 0.11). Training data were collected from the ground representing approximately 10% of the study area covering the entire spectral gradient of the classes. Separate test data were collected for validation.
LISS-III MS classified image using conventional Bayesian classifier is shown in figure 12 (a). Assuming that there are six (fixed) number of representative endmembers (pure pixels), the entire image was modeled in terms of those spectral components, extracted using N-FINDR algorithm (Winter, 1999) from MODIS images. In the absence of pure pixels, alternative algorithms (Plaza et al., 2004) can be used for endmember extraction, which is a limitation of N-FINDR. It may be noted that some objects (for example buildings with concrete roofs, tiled roofs, asphalt, etc.) exhibit high degrees of spectral heterogeneity representing variable endmembers. This intra-class spectral variation with variable endmembers can be addressed through techniques discussed in (Bateson et al., 2000; Song, 2005; Foody and Doan, 2007).
Abundance values were estimated for each pixel through unmixing and used as prior probabilities in HBC to classify LISS-III MS data (Fig. 12 (b)). Table 11 is the class statistics and table 12 indicates the producer’s and user’s accuracies. The overall accuracy and Kappa for HBC (93.54%, 0.91) is higher than Bayesian classifier (87.55%, 0.85). For any particular class, if the reference data has more pixels with correct label, the producer’s accuracy is higher and if the pixels with the incorrect label in classification result is less, its user’s accuracy is higher (Mingguo et al., 2009). Bayesian classifier wrongly classified many pixels belonging to waste/barren/fallow as builtup. Forest class was over-estimated and plantation was under-estimated by Bayesian classifier. The only minority class in the study area is water bodies. Classified image using conventional Bayesian classifier had 1.08% (8854 ha) of water bodies in the study area. After the ground visit, we found that there are not many water bodies and the extents of most individuals were < 2000m2. Therefore, only a few water bodies that had spatial extent ≥ 62500 m2, could be used as endmembers. The minimum detected water class was 5% using unmixing of LS-HSR data. It may have happened that the prior probability was unlikely for this class while classifying the LISS-III MS data using HBC. The classified image obtained from HBC showed 0.81% (66.20 ha) of water bodies. A few pixels were wrongly classified using HBC, therefore, the producer’s accuracy decreased from 90.91 (in conventional Bayesian classifier) to 88.18% (in HBC).

Figure 12: LISS-III MS classified images: (a) Bayesian classifier, (b) HBC.
Table 11: Class statistics from Bayesian and HBC for LISS-III data
Classifiers → |
Bayesian classifier |
HFC |
Class ↓ |
Ha |
% |
Ha |
% |
Agriculture |
155, 451 |
19.04 |
142931 |
17.51 |
Builtup |
139, 759 |
17.12 |
79280 |
9.71 |
Forest |
93, 241 |
11.42 |
55721 |
6.83 |
Plantation |
89,493 |
10.96 |
176132 |
21.58 |
Waste land |
329, 473 |
40.36 |
355587 |
43.56 |
Water bodies |
8854 |
1.08 |
66.20 |
0.81 |
Table 12: Accuracy assessment for LISS-III data
Classifiers → |
Bayesian classifier |
HBC |
Class ↓ |
PA* |
UA* |
PA* |
UA* |
Agriculture |
87.54 |
87.47 |
90.15 |
↑ |
95.56 |
↑ |
Builtup |
85.11 |
81.68 |
89.39 |
↑ |
98.33 |
↑ |
Forest |
85.71 |
88.73 |
92.61 |
↑ |
96.36 |
↑ |
Plantation |
84.44 |
91.73 |
95.95 |
↑ |
91.03 |
↓ |
Waste land |
88.03 |
90.37 |
98.67 |
↑ |
89.66 |
↓ |
Water bodies |
90.91 |
88.89 |
88.18 |
↓ |
97.00 |
↑ |
Average |
86.96 |
88.15 |
92.49 |
↑ |
94.66 |
↑ |
* PA – Producer’s Accuracy; UA – User’s Accuracy.
However, given the same set of training pixels for classification, the user’s accuracy has increased from 88.89 to 97%. Producer’s accuracy increased for agriculture (2.6%), builtup (4.3%), forest (7%), plantation (11.5%) and waste land (10.6%) and user’s accuracy increased for agriculture (8%), builtup (16.6%), forest (7.6%) and water bodies (8%) in HBC output. On the other hand, producer’s accuracy decreased (2.7%) for water bodies and user’s accuracy decreased (~0.7%) for plantation and waste land classes in agreement with the similar observations reported in Mingguo et al. (2009). HBC was intended to improve classification accuracies by correctly classifying pixels which were likely to be misclassified by Bayesian classifier. Therefore a cross comparison of the two classified images located the pixels that were assigned different class labels at the same location. These wrongly classified pixels when validated with ground data revealed a 6% (~1742832 pixels) improvement in classification by HBC.
In the second experiment, IKONOS MS data (4 bands of 4 m, acquired on November 24, 2004) of 700 x 700 size and Landsat ETM+ data (6 bands excluding Thermal and Panchromatic, of 30m, acquired on November 22, 2004) of 100 x 100 dimension were co-registered (RMSE - 0.09). Landsat pixels were resampled to 28 m so that 49 IKONOS pixels would fit in 1 Landsat pixel. The scenes correspond to Bangalore city, India near the central business district having race course, bus stand, railway lines, parks, builtup with concrete roofs, asbestos roofs, blue plastic roofs, coal tarred roads with flyovers and a few open areas (playground, walk ways, vacant land, etc.). Class proportions from Landsat image pixels were used as prior probabilities to classify the IKONOS MS images using HBC (Figure 13 (b)). The overall accuracy and Kappa for HBC (89.53%, 0.87) is higher than Bayesian classifier (80.46%, 0.69). Producer’s accuracy increased by 17% for concrete, asbestos, blue plastic roof and open area and decreased by 7% for vegetation in HBC (table 14). User’s accuracy increased by ~5.5% for all the classes in HBC. Bayesian classifier wrongly classified and overestimated many pixels belonging to open area as asbestos roof (table 13). Vegetation was overestimated by 9% using Bayesian classifier and open area was underestimated by ~15%. A cross comparison of the two classified images showed that 95733 pixels (0.33% of the study area) were differently classified by the two classifiers. Validation of these pixels showed an improvement of 9% by HBC, higher than accuracies reported in (Janssen and Middelkoop, 1992; Cetin et al., 1993; Strahler, 1980).
Table 13: Class statistics for IKONOS data
Classifiers → |
Bayesian classifier |
HBC |
Class ↓ |
Ha |
% |
Ha |
% |
Concrete roof |
346.67 |
44.34 |
356.18 |
45.56 |
Asbestos roof |
47.99 |
7.41 |
6.79 |
0.87 |
Blue plastic roof |
5.83 |
0.75 |
0.21 |
0.03 |
Vegetation |
329.72 |
42.18 |
260.01 |
33.26 |
Open area |
41.60 |
5.32 |
158.58 |
20.28 |
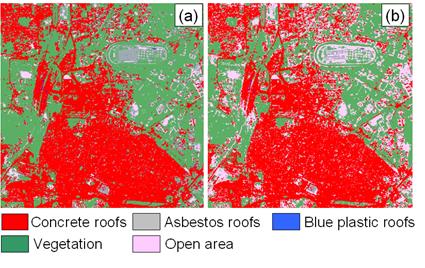
Figure 13: IKONOS classified images: (a) Bayesian classifier, (b) HBC.
Table 14: Accuracy assessment for IKONOS data
Classifiers → |
Bayesian classifier |
HBC |
Class ↓ |
PA |
UA |
PA |
UA |
Concrete roofs |
69.99 |
84.01 |
76.49 |
↑ |
93.89 |
↑ |
Asbestos roofs |
84.77 |
87.77 |
91.89 |
↑ |
94.46 |
↑ |
Vegetation |
94.21 |
87.55 |
87.24 |
↓ |
89.13 |
↑ |
Blue plastic roof |
84.33 |
81.17 |
97.00 |
↑ |
85.60 |
↑ |
Open area |
51.49 |
69.49 |
95.00 |
↑ |
74.22 |
↑ |
Average |
76.96 |
81.99 |
89.52 |
↑ |
87.46 |
↑ |
|
|
T.V Ramachandra,
Centre for Sustainable Technologies, Indian Institute of Science,
Bangalore 560 012, India.
Tel: 91-080-23600985 / 2293 3099/ 2293 2506,
Fax: 91-080-23601428 /23600085 /2360685 (CES TVR).
Web: http://ces.iisc.ac.in/energy, http://ces.iisc.ac.in/foss
|