Materials and Methods

Urban dynamics was analysed using temporal remote sensing data of the period 1973 to 2010. The time series spatial data acquired from Landsat Series Multispectral sensor (57.5m) and Thematic mapper (28.5m) sensors for the period 1973 to 2010 were downloaded from public domain (http://glcf.umiacs.umd.edu/data). Survey of India (SOI) topo-sheets of 1:50000 and 1:250000 scales were used to generate base layers of city boundary, etc.The process of the analysis is threefold as described in Figure 3, which includes preprocessing, analysis of land cover and land use, finally gradient wise zonal analysis of Delhi.

Figure 3: Procedure adopted for classifying the landscape and computation of metrics

• Preprocessing: Remote sensing data (Landsat series) for Delhi aquired for different time period were downloaded from Global Land Cover Facility (http://www.glcf.umd.edu/index.shtml) and (http://www.landcover.org/), United States Geological Survey (USGS) Earth Explorer (http://edcsns17.cr.usgs.gov/NewEarthExplorer/).The remote sensing data obtained were geo-referenced, geo-corrected, rectified and cropped pertaining to the study area. Geo-registration of remote sensing data (Landsat data) has been done using ground control points collected from the field using pre calibrated GPS (Global Positioning System) and also from known points (such as road intersections, etc.) collected from geo-referenced topographic maps published by the Survey of India. The Landsat satellite data of 1973 (with spatial resolution of 57.5 m x 57.5 m (nominal resolution) and 1989 - 2010 (28.5 m x 28.5 m (nominal resolution)) were resampled to 30m in order to maintain uniformity in spatial resolution across different time period. The study area includes the Delhi administrative area with 10 km buffer.

• Land Cover analysis: Land Cover analysis was performed to understand the changes in the vegetation cover during the study period in the study region. Normalised difference vegetation index (NDVI) was found suitable and was used for measuring vegetation cover. NDVI values ranges from values -1 to +1. Very low values of NDVI (-0.1 and below) correspond to soil or barren areas of rock, sand, or urban builtup. Zero indicates the water cover. Moderate values represent low density vegetation (0.1 to 0.3), while high values indicate thick canopy vegetation (0.6 to 0.8).

• Land use analysis: The method involves i) generation of False Colour Composite (FCC) of remote sensing data (bands – green, red and NIR). This helped in locating heterogeneous patches in the landscape ii) selection of training polygons (these correspond to heterogeneous patches in FCC) covering 15% of the study area and uniformly distributed over the entire study area, iii) loading these training polygons co-ordinates into pre-calibrated GPS, vi) collection of the corresponding attribute data (land use types) for these polygons from the field. GPS helped in locating respective training polygons in the field, iv) supplementing this information with Google Earth  v) 60% of the training data has been used for  classification, while the balance is used for validation or accuracy assessment.

  Land use analysis was carried out using supervised pattern classifier - Gaussian maximum likelihood algorithm. Remote sensing data was classified using signatures from training sites that include all the landuse types detailed in table 3.Mean and covariance matrix are computed using estimate of maximum likelihood estimator.This technique is proved superior classifier as it uses various classification decisions using probability and cost functions (Duda et al., 2000, Ramachandra et al., 2012b).

  Maximum Likelihood classifier is then used to classify the data using these signatures generated. This method is considered as one of the superior methods as it uses various classification decisions using probability and cost functions (Duda et al., 2000). Mean and covariance matrix are computed using estimate of maximum likelihood estimator. Land Use was computed using the temporal data through open source program GRASS - Geographic Resource Analysis Support System (http://ces.iisc.ernet.in/foss). Signatures were collected from field visit and help of Google earth. 60% of the total generated signatures were used in classification, 40% signatures were used in validation and accuracy assessment.  Classes of the resulting image were reclassed and recoded to form four land-use classes. The excessive noise in the classified images was removed by moving 3 X 3 median filter on it.

  Table 3: Land use classification categories

  Land use Class	Land uses included in the class
  Urban	This category includes residential area, industrial area, and all paved surfaces and mixed pixels having built up area.
  Water bodies	Tanks, Lakes, Reservoirs.
  Vegetation	Forest, Cropland, nurseries.
  Others	Rocks, quarry pits, open ground at building sites, kaccha roads.

• Accuracy assessment: These methods evaluate the performance of classifiers (Mitrakis et al., 2008).  This is done either through comparison of kappa coefficients (Congalton et al., 1983). For the purpose of accuracy assessment, a confusion matrix was calculated. Accuracy assesment, Kappa coefficient, are common measurements used in various publications to demonstrate the effectiveness of the classifications (Congalton, 1991; Lillesand & Kiefer, 2005).Recent remote sensing data (2010) was classified using the collected training samples. Statistical assessment of classifier performance based on the performance of spectral classification considering reference pixels is done which include computation of kappa (κ) statistics and overall (producer's and user's) accuracies. For earlier time data, training polygon along with attribute details were compiled from the historical published topographic maps, vegetation maps, revenue maps, etc.

• Zonal Analysis: City boundary along with the buffer region has been divided into 4 zones: North east, Southwest, Northwest and South east for further analysis as the urbanization is not uniform in all directions. As most of the definitions of a city or its growth is defined in directions it was considered more appropriate to divide the regions in 4 zones based on direction.  Zones were divided considering the Central pixel (Central Business district). The growth of the urban areas along with the agents of changesis understood in each zone separately through the computation of urban density for different periods.

• Division of these zones to concentric circles (Gradient Analysis): Each zone was divided into concentric circle of incrementing radius of 1 km radius from the center of the city, this analysis helped in visualising the process of change at local level and to understand the agents responsible for changes. This helps in identifying the causal factors and locations experiencing various levels (sprawl, compact growth, etc.) of urbanization in response to the economic, social and political forces. This approach (zones, concentric circles) also helps in visualizing the forms of urban sprawl (low density, ribbon, leaf-frog development). The built up density in each circle is monitored overtime using time series analysis. This helps the city administration in understanding the urbanization dynamics to provide appropriate infrastructure and basic amenities.

• Shannon’s Entropy: Further to understand the growth of the urban area in specific zone and to understand if the urban area is compact or divergent the Shannon’s entropy (Sudhira et al., 2004; Ramachandra et al., 2012a) was computed for each zones. Shannon’s entropy (Hn) given in equation 1, explains clearly the development process and its characteristics. 

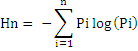                           …..(1)

  Where Pi is the proportion of the built-up in the ith concentric circle. As per Shannon’s Entropy, if the distribution is maximally concentrated in one circle the lowest value zero will be obtained. Conversely, if it is an even distribution among the concentric circles will be given maximum of log n.

• Computation of spatial metrics: Spatial metrics are helpful to quantify spatial characteristics of the landscape. Selected spatial metrics were used to anlayse and understand the urban dynamics, FRAGSTATS (McGarigal and Marks in 1995) was used to compute metrics at three levels: patch level, class level and landscape level. Annexure I(a-d). below gives the list of the metrics along with their description considered for the study.

  Area metrics: Area metrics quantifies the composition of the landscape and provides information about the area occupied by various patches in the landscape. Annexure Iaprovides description of area metrics.

  Annexure Ia: Description of the Area metrics

  Indicator	Formula	Description
  Class Area (CA)	Range: CA>0, without limit	CA shows how much of the landscape is comprised of one patch type. Equals the sum of the areas (m2) of all patches of the corresponding patch type, divided by 10,000. aij area (m2) of patch ij.
  Number of patches (Built-up) (NP)	Range: NP≥ 1	NP equals the number of patches of the corresponding patch type.  ni is the number of patches of a particular type.
  Percentage of landscape  (Built-up) (PLAND)	Range: 0<%Land≤ 100	PLAND equals the percentage the landscape comprised of the corresponding patch type. aij = area (m2) of patch ij. A =  total landscape area (m2).
  Patch Density (PD)	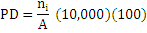Range: PD> 0	PD is the number of patch of urban patch divided by total landscape area.
  Largest patch Index (Built-up) (LPI)	) Range: 0< LPI≤ 100	LPI approaches 0 when the largest patch of the built-up patch becomes increasingly small and LPI = 1 when the entire landscape of the patch type of the built-up class.
  Mean Patch Size (Class/Landscape) (MPS)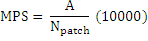	Range: MPS > 0, without limit	MPS equals the sum of the areas (m2) of all patches of the corresponding patch type, divided by the number of patches of the same type, divided by 10000.
  Patch  Area  Distribution coefficient of variance (Class level) (PADCV)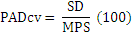	Range: PADCV ≥ 0, without limit	Calculates coefficient of variation of patch area on a raster map.

  Shape Metrics: Shape metricslisted in Annexure Ib quantify the landscape configuration by measuring shape complexity of patches at patch, class and landscape level.  Shape is a difficult parameter to quantify concisely in a metric (McGarigal and Marks, 1994). All the shape indices are based on perimeter to area ratio and thus they help in interpreting irregularities in urban patches.

  Annexure Ib: Metrics to compute shape complexity of patches (Source: Mc Garigal and Marks, 1994)

  Indicator	Formula	Description
  Mean Shape Index (Class level) (MSI)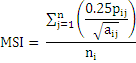	Range:  MSI > 1, without limit.	It measures the average patch shape for a particular class. MN (Mean) equals the sum, across all patches of the corresponding patch type, of the corresponding patch metric values, divided by the number of patches of the same type.
  Normalised landscape shape Index (NLSI)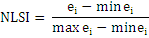	Range: 0 to 1	Normalized Landscape shape index is the normalized version of the landscape shape index (LSI) and, as such, provides a simple measure of class aggregation or clumpedness.

  Edge/Border Metrics: Edge metrics (Annexure Ic) quantify length and distribution of the amount of edge between patches (Frohn and Hao, 2006). They represent landscape configuration, even though they are not spatially explicit at all (McGarigal and Marks, 1995). These edge attributes can provide critical information for quantifying and understanding urban and landscape fragmentation.

  Annexure Ic: Quantification of urban and landscape fragmentation through selected Edge/ Border Metrics (Source: McGarigal and Marks. 1994).

  Indicator	Formula	Description
  Perimeter-Area Fractal dimension (PAFRAC)	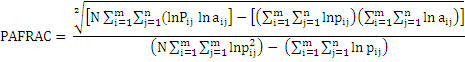Range: 1 < PAFRAC  < 2,	PAFRAC greater than 1 indicating the increase in shape complexity.

  Compactness Metrics/Contagion and Interspersion Metrics: Compaction is the formation of rounded patches in a circular shape that makes them more compact (Aguileraet al., 2011). These metrics liosted in Annexure Id quantify landscape configuration. Compactness Metrics is the measure of individual patch shape and fragmentation of overall landscape.

  Annexure Id: Compactness metrics to assess individual patch shape and fragmentation of overall landscape

  Indicator	Formula	Description
  Area- weighted Euclidean Nearest Neighbor Distance Distribution (ENN_AM)	ENN = hij	Where hij= distance from patch ij to nearest neighboring patch of the same type based on patch edge-to-edge distance.
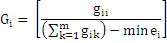
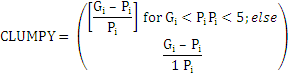
  Clumpiness Index (Clumpy)	Range:  Clumpiness ranges from -1 to 1	Clumpy = -1 when the focal patch type is maximally disaggregated, Clumpy = 0 when the focal patch is distributed randomly and approaches 1, when patch type is maximally aggregated.
  Interspersion & Juxtaposition Index (Landscape level) (IJI)	Range: 0 < IJI ≤ 100	eik = total length (m) of edge in landscape between patch types I and k. m= number of patch type present in landscape.