1 . 1 Models in Space and Time

The advances in geo-informatics coupled with the availability of spatial and temporal information from remotely sensed data have aided to investigate and model the environmental systems. These models are executed for different scenarios or alternatives depending upon the specific objectives. Modelling the spatial and temporal dimensions has been an intense subject of discussion and study for philosophy, mathematics, geography and cognitive science (Claramunt and Jiang, 2001).

The Geographic Information System (GIS) has until now offered storage, retrieval and analysis of spatial and temporal databases. This has helped in modelling of the different environmental processes in the spatial and temporal dimensions. Different models for representing the spatial and temporal phenomenon have evolved from the traditional Location-based/Snapshot models to Entity-based models (Object-oriented approach) to Event-based models to Process-based models and so on. Inspite of the continuous developments in the representations of the geo-spatial data along with their temporal attributes, these systems with the goal of gaining insights about cause-effect relationships are not yet ready to answer the questions of patterns of change through time (Peuquet, 1999).

A simulation is the imitation of the operation of a real-world process or system over time (Banks and Carson, 1984). Simulation is the key technology for describing, assessing, analysing, forecasting, etc. the dynamics of real, planned or virtual systems (Schulze et. al., 2002). An important growing concern in the geo-informatics community is the simulation of the environmental processes using the different models in the spatial and temporal dimensions within a GIS. In the spatial domain, modelling and subsequent simulations have been extensively attempted for the various processes involved in environment, like the meteorology, hydrology, air pollution dispersion, urban growth, land-use / land-cover dynamics etc. The types of mathematical models are categorized by Cellier (1991) into three types based on the different interpretations of time. The first type is the set of continuous-time models, which are characterized by the fact that, within a finite time span, the state variables change their values infinitely often. These continuous-time models are typically represented by the differential equations. The second type is the set of discrete-time models, wherein the time axis is discretized. These models are commonly represented as sets of difference equations when the discretization is equally spaced. The last type of models is the set of discrete-event type models, wherein the time axis of such models are continuous (real, instead of integer). The discrete-event model differs from the continuous-time model by the fact that within a finite time-span only a finite number of state changes can occur.

Describing the approaches of dynamic land-use models, Liu and Anderson (2004) categorize them as process-based and transition-based modelling. Process-based models are known to describe the causality between the different components of the system explicitly. Transition-based models use probability or similar terms to summarize the changes happened over a time interval.

Mostly, simulations are run based on the models or equations by numerical methods rather than by analytical methods (Banks and Carson, 1984). Analytical methods employ the deductive reasoning of mathematics to solve the equation representing the model . For example, differential calculus can be used to determine the shortest route in a network model. Numerical methods employ computational procedures to ‘solve' mathematical models. In the case of simulations, which employ numerical methods, models are ‘run' than solved; that is an artificial history of the system is generated based on the model assumptions, and observations are collected to be analysed and to estimate the true system performance measures (Banks and Carson, 1984). The validation of a model is the determination of the model is an accurate representation of the system. Validation is usually achieved through the calibration of the model, an iterative process of comparing the model to actual system behaviour and using the discrepancies of the two, and the insights gained to improve the model.

Modelling and simulations in the spatial domain is now extensively done using the techniques of Cellular Automata (CA), although t here are different approaches to model processes in space and time including the geo-statistical approaches, differential equations, etc. Simulations undertaken by CA models and geo-statistical techniques are of numerical type. CA is a cell-based approach to model processes in a two–dimensional space. Benenson and Torrens (2003) define an automaton as a discrete entity, which has some form of input and internal states. These states can change over time according to a set of rules to determine a new state in a subsequent time step. These rules control the transformation of a cell state to another cell state over the specific period of time depending on the neighbourhood of the cells. A detailed account on CA is discussed in the next chapter.

The geo-statistical modelling by Kriging is another numerical method for spatial interpolation or estimation. Kriging, to some extent has similarities to a CA, that there is a function driving the interpolation. By definition of Kriging, it is a method of interpolation, which predicts unknown values from data observed at known locations. This method uses variogram to express the spatial variation, and it minimizes the error of predicted values, which are estimated by spatial distribution of the predicted values. In essence, Kriging uses data points that are minimal or less or sparsely sampled. In this regard, CA approaches assume that entire data set although discrete in space has continuous set of data values in cells and not only a few samples. Further CA offers opportunity to address the temporal dimension at least in its discrete nature at regular time steps, which are not so capable of being handled in other techniques to model processes of space and time. Thus CA has emerged as popular method for modelling processes in space and time.

In CA based modelling the temporal variability of spatio-temporal processes is less addressed than its spatial counterpart. CA based models are used for studying temporal dynamics (Clarke and Gaydos, 1998; Liu and Anderson, 2004) wherein the temporal dimension is mostly considered as duration and discrete. Normally in a CA model, the transitions take place from time t to time t+1 and would ideally simulate the physical states between time t=0 and t+1 (Batty and Jiang, 1999). Although time can be discretized at higher scale (discrete-time stepped), the state changes of the CA for certain transition rules can be assumed to be within specific time only and not at all the discretized time units. In certain situations there can be more transition rules for various state changes at varied time units underlying the importance of the events that take place based on the transitions and not all transitions that may or may not happen at every time step. In case of CA, the state changes are only within the discrete set of time, thus they are a fit case of both discrete-time model and discrete-event model.

Though CA based models have been used for simulating various dynamics extensively, CA are considered as immobile geographical automata (Benenson and Torrens, 2003). They are immobile because individual automata are not free to move in the space in which they reside; all spatial movement takes place through the diffusion of information through neighbourhoods. In addition, Batty and Jiang (2000) argue that the development of spatial interaction in spaces wider than the neighbourhood itself and in enabling the model dynamics to take account of system-wide conservation constraints, are usually destroyed by the CA transitions. Most importantly transition rules account only for the states and neighbourhood and not for externalities driving the processes.

Modelling of land-use / land-cover dynamics in both space and time is bounded by various causal factors driving the changes that can have varied relations in space and time apart from the inherent physical state dynamics. A specific use-case of involving such a land-use / land-cover dynamics considered in this research is the dynamics of urban sprawl. The phenomenon of urban sprawl is characterized by the uncontrolled or uncoordinated growth of the built-up area in the outskirts of a city or along the highways. The inherent causal factors and dynamics involved in the rapid changes occurring in the land-use / land-cover due to urban sprawl is considered as a fit case to apply the CA models for simulating for future scenarios. Typically, the CA models need to account for the external drivers that also drive a land-use / land cover change which are not accounted in the transition rules of the automata. Certain externalities can be system wide or specific to certain locations, for which the CA models have to evolve to address such requirements. Further there are also different significant processes that take place in the region in question, apart from those represented in the CA model. The new wave of research is driving towards integrating the agent-based models (multi-agent systems) with the CA models, such as in the case of modelling land-use / land cover dynamics by incorporating different drivers / agents involved.

The aim of agent design is to create a program, which interacts `intelligently' with its environment. The term ‘agent' is usually applied to describe self-contained programs, which can control their own actions based on their perceptions of their operating environment. The key hallmarks of agent-hood are autonomy, social ability, responsiveness, and pro-activeness (Jennings and Wooldridge, 1996). Agents, have their origins in software engineering and artificial intelligence where they are used in networking, communications, etc. An agent is an encapsulated computer system that is situated in some environment and that is capable of flexible, autonomous action in that environment in order to meet its design objectives.

The initial application of agent-based models within a GIS was made in studying the dynamics of pedestrian behaviour in streets (Schelhorn et al., 1999). As such agent-based models have been used to model the discrete dynamics of small-scale spatial events for mobility in carnivals and street parades (Batty, Desyllas and Duxbury, 2003). Thus, agent-based models are mobile geographical automata with transition rules.

The combination of CA and agent-based models has enabled to address the interactions in space and time (Batty and Jiang, 1999) by the representation of different behaviours (drivers) as objects. Semboloni et al., (2004) present an interactive multi-agent simulation model on the web, CityDev, which is an interactive, dynamic model that can interact with the user on the web.

Object-oriented approaches to cells, where cells represent land parcels, administrative areas, or even individual buildings, almost invariably require non-regular lattices, but may ease the problem of defining transition rules (O'Sullivan and Torrens, 2000). The agent-based models would have all the characteristics of cellular automata, but, unlike the cellular automata, agents in an agent-based model would be programmed for spatial mobility within the regions they inhabit. The focus here is on to develop the framework for integrating the CA models and agent-based models validating the same for the use case of urban sprawl dynamics.

To depict the fusion of cellular automata and multi-agent systems in a spatial context for simulating discrete, dynamic and action-oriented spatial systems, Benenson and Torrens (2003) propose the term Geographic Automata Systems (GAS). The GAS framework d efines the automata collectively considering, type of automata, states, transition rules, location, movement rules, neighbours, and neighbourhood transition rules. Thus, the GAS framework addresses the fusion of CA and ABM in a spatial context, by tight coupling of GAS with GIS. With this, there can be many automata with different scales for space and time, defined based on the process/phenomenon in question. However, when there are two or more automata waiting to be executed at the same space and time, such cases are handled only by synchronous or asynchronous updating.

Furthermore, the management of time in the GAS framework is less advanced to handle multiple simulations simultaneously, for which their framework uses ‘synchronous' and ‘asynchronous' updating. The GAS framework uses the Object-based Environment for Urban Systems (OBEUS) for validation. In the ‘s ynchronous' updating – “all automata are assumed to change simultaneously and conflicts can arise when agents compete over limited resources. Resolution of these conflicts depends on the model's context, a decision OBEUS leaves to the modeller”. Also in case of ‘asynchronous' updating – “automata change in sequence, with each observing a geographic reality left by the previous automata. Conflicts between automata are thereby resolved; but the order of updating is critical as it may influence results. OBEUS demands the modeller sets up an order of automata updating according to a template: randomly, sequence in order of some characteristic” (Benenson et al., 2004).

1.2 Scales and Representations of Models in Space and Time

The scales and representations of models in space and time can be addressed depending on the number of dimensions in which they are looked at. The current research perceives the models in space in two-dimensional surface and that of time are considered to be linear. According to Goodchild (2001) the scale implies the level of spatial detail or spatial resolution, often defined as the shortest distance over which the change is recorded and thus having some units. In the geo-spatial representations of models in the raster forms in a lattice structure, the cell side corresponds to spatial resolution. However, the raster representations can be of regular lattice as in the case of remote sensing images or irregular lattice structures like that of an triangulated irregular network model. The universally followed scale for planar models in space is the metric system with the units of meters. However in the geographic space, the earth is considered as an ellipsoid and so specific systems of representation have evolved in two-dimensional space as coordinate systems and datums as references for the measurement of height of the surface on the earth. Among the coordinate systems is the Universal Transverse Mercator (UTM) projection in meters and the geographic coordinates as latitudes and longitudes. As there are different possible geometries, projections, coordinate systems and datums defined for the representation of geographic feature in space, the Open Geo-spatial Consortium (OGC) has adopted a conceptual schema under the Abstract Specification Topic 1 – Feature Geometry, which is identical with the ISO 19107 – Geographic Information – Spatial Schema (OGC, 2003).

On the temporal aspects of scales, the time is linearly discretized in equally spaced intervals as (nano-, micro-, milli-) seconds that make up the minutes, hours, days, weeks, months, years, etc. Obviously most models have a temporal resolution that falls under any one of the classes above mentioned. While modelling the geographic processes, the scales of these features modelled can vary in space and time. And so, for an effective and meaningful simulation of these models, the synchronization of the different models has to be addressed to obtain tangible results in both space and time. The spatial synchronization would refer to the process of coupling the models with different geographic spatial scales to an appropriate scale, for example resampling an image for a particular spatial resolution. In the similar context the temporal synchronizations would address the coupling of different time-variant models. Nevertheless, most processes in the environmental systems take place at their own respective scales in both space and time. Even though if certain processes were individually modelled using CA and/or agent-based models, these models wouldn't have a common spatial and temporal resolution. Although, the geo-spatial community has for long until now attempted to model and simulate these different processes on the desktop aided by the advances in the computational capabilities, a significant challenge faced by the geo-spatial community is the need of dynamic systems for modelling and simulation capable of integrating or synchronizing the different models of environmental processes at their respective scales.

In the case of land use / land cover dynamics involving an urban system, three levels of change processes can be identified according to their time scale: slow processes which take 3–5 years or longer to complete and affect the physical structure of a city, e.g. industrial, residential, and transport construction; medium processes such as economic, demographic, and technological changes which affect the usage of the physical structures; and fast processes completed in less than a year, such as mobility of labour, goods, and information (Wegener, 1994). All processes would have their own respective start and end time apart from the spatial extents they are going to affect. Each of these individual and/or group of processes can be thought of as distributed simulation systems as an analogy to the computer science and engineering domain. Thus a typical framework for simulation should be addressing the synchronization of different models modelled using CA and/or agent-based models at appropriate spatio-temporal scales. In this backdrop the upcoming framework relies on the specifications adopted by the OGC to promote the interoperability and reusability of the simulations.

In the modelling and simulation domains of the computer science and engineering numerous advances are made with respect to synchronization of such distributed simulations and parallel simulations. A key distinction is that the modelling and simulation community are able to achieve the synchronization of the time-variant simulation models using the standardized simulation framework, the High Level Architecture (HLA), an IEEE standard (1516), initially developed by the United States Department of Defence (Dahmann, Fujimoto and Weatherly, 1998; IEEE, 2000).

HLA is the architecture for reuse and interoperation of simulations. The intent of the HLA is to provide a structure that will support reuse of capabilities available in different simulations, ultimately reducing the cost and time required to create a synthetic environment for a new purpose and providing developers the option of distributed collaborative development of complex simulation applications. Thus the HLA offers a federation approach and addresses the interoperability and reuse of individual components. In order to facilitate interoperability, each member (federate) of a distributed simulation (federation) is equipped with appropriate interfaces to interact via a run-time infrastructure.

With the available architecture (HLA) for distributed simulations in the computer science and engineering domain, the current direction of research is to enable the spatial component based on this architecture so as to address spatial synchronizations apart from the temporal synchronization already available. Moreover, an ideal framework for simulation should be reusable and interoperable for different use cases and multidisciplinary research teams thereby minimizing the cost of effort and time for modellers to rebuild a simulation framework specific to their use case or research areas. An interoperable simulation framework should facilitate the modeller to utilize the framework more flexibly by allowing an open system or on a common platform. An open system is an information processing system that complies with the requirements of open systems interconnection (OSI) standards in communication with other such systems. An open systems interconnection (OSI) defines the accepted international standard by which open systems should communicate with each other. It takes the form of a seven-layer model of network architecture, with each layer performing a different function. OSI is used to develop interfaces and integrate two dissimilar systems, for example, PCs and UNIX or UNIX and mainframes. The OSI is sponsored by the International Standards Organization (ISO) (Patterson & Gittings, 1996). In the geo-spatial modelling domain, the proposed framework is to comply with the open system interconnection standards for facilitating the functioning of the framework in any system.

The focus of this research is on overcoming the limitations of the CA models by integrating CA with the agent-based models considering the issues of scales for synchronization of these models in space and time. Consequently and conceptually, this research framework is looking at coupling the agents and CA models, and incorporating a geo-spatial analyser (GSA) to handle the spatial synchronization and the HLA framework to handle the temporal synchronization, the discreteness in both spatial and temporal scales would be more flexible and robust to handle the issues arising out of multiple discrete-time stepped simulations.

1.3 Objective

The main objective is to develop the framework for the integration of agent-based and a cellular automaton model. This investigation will integrate agent-based models and CA model for synchronizing in their respective spatial and temporal scales. Specific questions addressed are:

1 What are the requisite conditions and methods for integrating agent-based models and CA at appropriate scales?

2 What are the requirements for framework to be interoperable and reusable for different processes?

3 What are the calibration and validation techniques (accuracy assessment methods) for evaluating and ensuring the usability of the simulations?

1.4 Method

The prerequisites for the integration of agents and CA were identified through literature review. Analytical solutions for the integration of the agent-based models over the CA as Agent-Based Cellular Automata (ABCA) are developed. A key aspect for the integration is to synchronize models at appropriate spatial and temporal resolutions. Thus, for managing the spatial component for different simulations, a Geo-Spatial Analyser is proposed. The detailed functionalities of this are discussed in the subsequent chapters. The utility of High Level Architecture (HLA) developed by the United States Department of Defence, which provides a time-variant framework for distributed simulations, is incorporated in the simulation framework. The HLA, which is also an IEEE standard (IEEE 1516) uses a federation approach and facilitates interoperability of distributed simulators. The current research addresses the synchronization of the different individual agent-based models in both space and time over a CA. The general simulation framework is shown in Figure 1. In such a framework, the final transition rules of a CA would be derived from the interactions among different agents. Thus the agent-based model would operate on top of a CA layer where agents' respond or initiate state transitions in the CA. The research approach is outlined in Figure 2. The dynamics of urban sprawl is considered as the use case. In case of urban sprawl, the external driving process like infrastructure development process can be an agent.

1.5 Structure of the Document

The report is organised in six chapters. The second chapter describes the theoretical background of the CA models and the agent-based models in detail. In the third chapter, the framework for the integration of CA models and agent-based models outlining the conditions requisite for the integration are addressed along with the concepts of Geo-Spatial Analyser and the HLA framework. This chapter includes the descriptions on the functionalities of the proposed GSA and the HLA architecture. The application of such a framework for the use case of urban sprawl is the fourth chapter. This chapter also describes the study area in question and the drivers considered as agents. A generalized CA model is developed in the simulation framework. The fifth chapter describes the results and discussion after implementing the framework at the prototype level. The calibration and validation of such simulations is also taken up for discussion. The sixth chapter concludes with the scope for further research in the area.

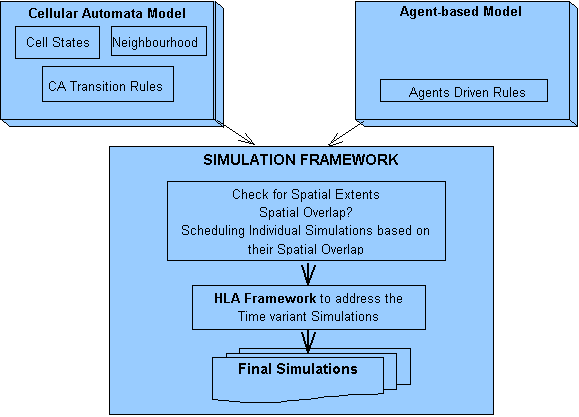
Figure 1.1:Framework for the Simulations Integrating the CA and Agent-based Models

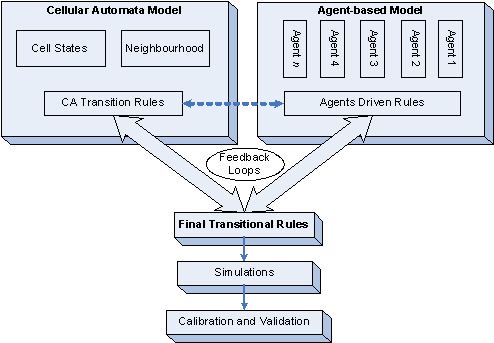
Figure 1.2: Outline of the Research Approach