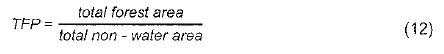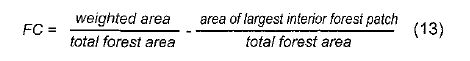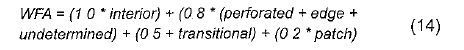Methods
- Orthogonal Subspace Projection (OSP) – Pixel usually contain contributions from more than one class, when object size is smaller than the pixel resolution (mixed pixels) except in higher spatial resolution data. Standard classification techniques, which attribute a single class to the entire pixel, are therefore inappropriate to low spatial resolution satellite images from space-borne sensors. This motivates the development of algorithms which unmix the coarse spatial data or, in other words, perform classification at a sub-pixel level. The main objective is to find out the proportion of each category in a given pixel, or in other words, unmix the pixel to identify the categories present within the pixel. In order to address this problem, unmixing techniques have been developed to exploit sub-pixel level information for image analysis [5], where sub-pixel class composition is estimated through the use of techniques, such as linear mixture modeling [6], supervised fuzzy-c means classification and artificial neural networks, etc.
Linear unmixing is based on an assumption that the spectral radiance measured by the sensor consists of the radiances reflected collectively in proportion to the sub-pixel area covered by each material. Let K be the number of spectral bands in the multispectral / superspectral data set, and P, the number of distinct classes of objects in the physical scene. Associated with each pixel is a K-dimensional vector y whose components are the gray values corresponding to the K bands. Let E = [e1, e2,…, ep], where {ei} is a column vector representing the spectral signature of the ith target material or category. The column vectors of the K x P matrix E are called end-members. For a given pixel, the abundance fraction of the pth target material present in a pixel is denoted by αp, and these values are the components of the P- dimensional abundance vector α. Assuming the linear mixture model, the observation vector y is related to E by
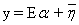 (1) (1)
where 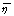 accounts for the measurement noise. We further assume that the components of the noise vector accounts for the measurement noise. We further assume that the components of the noise vector 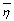 are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is 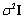 , where , where 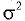 is the variance, and I is K x K identity matrix. The conventional approach [7] to extract the abundance values is to minimise is the variance, and I is K x K identity matrix. The conventional approach [7] to extract the abundance values is to minimise 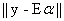 , and the estimate for the abundance is , and the estimate for the abundance is
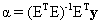 (2) (2)
which is termed as the Unconstrained Least Squares (ULS) estimate of the abundance. Imposing the sum-to-one constraint on the abundance values while minimising 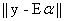 , gives the Constrained Least Squares (CLS) estimate of the abundance as, , gives the Constrained Least Squares (CLS) estimate of the abundance as,
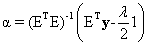 (3) (3)
where,
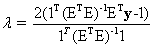 (4) (4)
Chang (2005) [8] came up with a technique called Orthogonal Subspace Projection (OSP) in the signal processing domain, which is used here as a classification technique based on two aspects: 1) how to best utilise the target knowledge provided a priori and 2) how to effectively make use of numerous spectral bands. Briefly, the technique involves (i) finding an operator which eliminates undesired spectral signatures, and then (ii) choosing a vector operator which maximises the signal to noise ratio (SNR) of the residual spectral signature. In order to find the abundance of the pth target material (αp), let the corresponding spectral signature of the desired target material be denoted as d. The term Eα in equation (1) can be rewritten to separate the desired spectral signature d from the rest as:
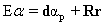 (5) (5)
where r contains the abundance of the rest of the end-members, and R is a K x P - 1 matrix containing the columns of E except for the column vector d. We rewrite (1) as
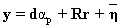 . (6) . (6)
The interfering signatures present in R can be removed from (6) by the operator,
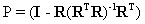 (7) (7)
which is used to project the vector y into a space orthogonal to the space spanned by the interfering spectral signatures. Therefore, operating on y with P, and noting that PR = 0, we get
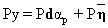 . (8) . (8)
The next step is to find an operator wT which maximizes the SNR given by
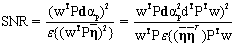 |
(9) |
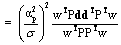 |
Maximizing the SNR leads to the generalized eigenvalue problem: 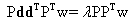 . .
The eigenvector corresponding to the maximum eigenvalue is the vector ‘w’. It can be shown that the w which maximises the SNR is given by
w = kd. (10)
Therefore, an optimal estimate of αp is given by
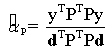 (11) (11)
In the absence of noise, the estimate matches with the exact value as in (6). The value of α is the abundance of the pth class (in an abundance map) ranging from 0 to 1 in any given pixel. 0 indicates absence of a particular class and 1 indicates full presence of that class in that particular pixel. There are as many abundance maps as the number of classes. Intermediate values between 0 and 1 may represent a fraction of that class. If the objective is to map the impervious surface, then OSP renders an impervious surface abundance map, where each abundance pixel shows the proportion of impervious material (buildings / houses / roads / paved surfaces, etc.) in that pixel.
Forest fragmentation – Forest fragmentation is the process whereby a large, continuous area of forest is both reduced in area and divided into two or more fragments. The decline in the size of the forest and the increasing isolation between the two remnant patches of the forest has been the major cause of declining biodiversity [9]. The primary concern is direct loss of forest area, and all disturbed forests are subject to “edge effects” of one kind or another. Forest fragmentation is of additional concern, insofar as the edge effect is mitigated by the residual spatial pattern [10].
Land cover (LC) map indicate only the location and type of forest, and further analysis is needed to quantify the forest fragmentation. Total extent of forest and its occurrence as adjacent pixels, fixed-area windows surrounding each forest pixel is used for calculating type of fragmentation. The result is stored at the location of the centre pixel. Thus, a pixel value in the derived map refers to between-pixel fragmentation around the corresponding forest location. As an example [11] if Pf is the proportion of pixels in the window that are forested and Pff is the proportion of all adjacent (cardinal directions only) pixel pairs that include at least one forest pixel, for which both pixels are forested then, Pff estimates the conditional probability that, given a pixel of forest, its neighbour is also forest. The six fragmentation model that identifies six fragmentation categories are: (1) interior, for which Pf = 1.0; (2), patch, Pf < 0.4; (3) transtitional, 0.4 < Pf < 0.6; (4) edge, Pf > 0.6 and Pf-Pff > 0; (5) perforated, Pf > 0.6 and Pf-Pff < 0, and (6) undetermined, Pf > 0.6 and Pf = Pff.
When Pff is larger than Pf, the implication is that forest is clumped; the probability that an immediate neighbour is also forest is greater than the average probability of forest within the window. Conversely, when Pff is smaller than Pf, the implication is that whatever is nonforest, is clumped. The difference (Pf - Pff) characterizes a gradient from forest clumping (edge) to nonforest clumping (perforated). When Pff = Pf, the model cannot distinguish forest or nonforest clumping. The case of Pf = 1 (interior) represents a completely forested window for which Pff must be 1.
Forest fragmentation indices [12] have two parts: (1) Total forest proportion (TFP) and Forest continuity (FC). TFP provides a basic assessment of forest cover in a region ranging from 0 to 1. FC value examines only the forested areas within the analysis region. Its measure specifically utilises the results from the forest fragmentation model.
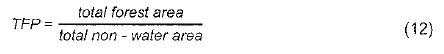
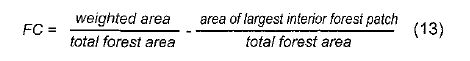
Weighted values for the weighted forest area (WFA) are derived from the median Pf value for each fragmentation class (equation 14):
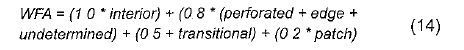
The rationale is that, given two regions of equal forest cover, the one with more interior forest would have a higher weighted area, and thus be less fragmented. To separate further regions based on the level of fragmentation, the weight area ratio is multiplied by the ratio of the largest interior forest patch to total forest area for the region. FC ranges from 0 to 1.
- Urban Dynamics Characterisation – An urban dynamics model has spatially detailed data with fine spatial grain, examines the whole landscape and assesses urban growth in all areas, avoids spatial averaging, maintains spatial pattern and configuration, and is consistent over time. The urban growth model used here is based on the modified forest fragmentation model developed by Ritters et al., (2000) [13]. The urban dynamics model uses urban and non-urban classes to create fragmentation image instead of forest and non-forest in forest fragmentation model. Input data consist of multi-dates LC with a minimum of three classes; urban (developed), non-urban (non-developed), and water. Instead of using a forest versus non-forest binary image to create a forest fragmentation map, the first step of the urban growth model uses a non-developed versus developed image to create a “non-developed” fragmentation image. The single date fragmentation map consist of three “fragmented” classes that are combination of the five classes previously described (interior, patch, transitional, edge and perforated). The first is interior, which occurs when all pixels in a 3 x 3 window are non-developed. The second class is perforated, which occurs when between 60 % and less than 100 % of pixels in a 3 x 3 window are non-developed. The final class is patch, which occurs when fewer than 60 % of pixels in a 3 x 3 window are non-developed. Two dates of fragmentation maps are used to create change map. There are three types of change classes – the first type consists of no change classes (including developed, water and interior), the second type includes improbable changes, likely due to classification error, and the third type consists of classes that represent urban growth. The classes that indicate urban growth are outlined in table 1 along with their corresponding urban growth classes. The change classes determine the type of urban growth. Infill is the development of a small area surrounded by existing developed land. Expansion is the spreading out of urban LC from existing developed land. Outlying growth is an interior pixel that changes to developed, and is further classified as either isolated, linear branching, or clustered branching (see table 1).
Table 1: Change classes that represent urban growth and the corresponding growth types [13]
| Significant Change Classes |
Type of Growth |
| Patch to Developed |
Infill Growth |
| Perforated to Developed |
Expansion Growth |
| Interior to Developed |
Outlying Growth:
- Isolated Growth,
- Linear Branching Growth,
- Clustered Branching Growth
|
Their distinction is made using a set of rules. An isolated growth is defined as a new, small area of construction surrounded by non-urban land and some distance from other developed areas. A linear branching growth is a road, corridor, or linear development surrounded by non-urban land and some distance from other urban areas. A clustered branching growth is indicative of a new, large and dense development in a previously undeveloped area. The urban growth model produces an urban growth map, which consists of five types of growth as well as developed land, water, and non-developed land. |


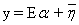 (1)
(1)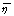 accounts for the measurement noise. We further assume that the components of the noise vector
accounts for the measurement noise. We further assume that the components of the noise vector 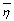 are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is
are zero-mean random variables that are independent and identically distributed. Therefore, the covariance matrix of the noise vector is 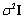 , where
, where 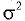 is the variance, and I is K x K identity matrix. The conventional approach [7] to extract the abundance values is to minimise
is the variance, and I is K x K identity matrix. The conventional approach [7] to extract the abundance values is to minimise 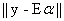 , and the estimate for the abundance is
, and the estimate for the abundance is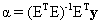 (2)
(2)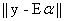 , gives the Constrained Least Squares (CLS) estimate of the abundance as,
, gives the Constrained Least Squares (CLS) estimate of the abundance as,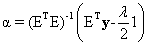 (3)
(3)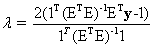 (4)
(4)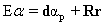 (5)
(5) 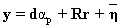 . (6)
. (6)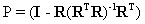 (7)
(7) 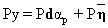 . (8)
. (8)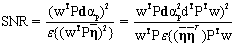
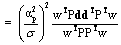
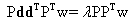 .
.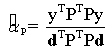 (11)
(11)