Home           Key speaker

Y.R. Rao and C.R. Murthy National Water Research InstituteBurlington, Ontario, Canada
Email: Ram.Yerubandi@ec.gc.ca

This paper discusses several physical processes that are relevant to water quality and sustainable management of small and large lakes. Knowledge of water movements is important because circulation influences the distribution of dissolved substances, nutrients, microorganisms and plankton. Although there is a tremendous amount of variability in the origins of a lake (natural) and a reservoir or impoundment (artificial), they share several common physical, chemical and biological characteristics . In particular, reservoirs have controlled outflow, whereas the lakes are uncontrolled. In addition to these aspects, the physical limnology of these water bodies are governed by the shape and size of the basin. Two aspects of size that have a strong bearing on water quality are residence time and depth. Shallow lakes (<10 m) are generally well-mixed, and deeper lakes (>10 m) are often subject to thermal stratification during certain times of the year. Therefore, the water balance of a lake or reservoir  generally depends on the inflow, outflow, groundwater flow, precipitation, evaporation over the water shed region of the lake. Discussion of large scale water motions includes water levels, seiches, currents, waves and turbulence. Wind, solar radiation, stratification, earth’s rotation are important forces causing water movements of lakes.

 Formation of water bodies may occur due to several reasons. Natural lake systems were generally formed during the ice ages because of tectonic or volcanic activities. In contrast man induced developmental activities are responsible for ever-increasing number of reservoirs and artificial impoundments. In these cases we have taken advantage of natural topographic characteristics which with minor modifications like construction of dams or embankments lend themselves to large storage facilities of freshwater. Drainage basins of reservoirs are much larger in relation to the lake surface areas. Because reservoirs are formed almost always in river valleys and at the base of the drainage basins, the morphometry of reservoir basins is usually narrow and elongated. Whether artificially or naturally created, all lakes share several common physical, chemical and biological characteristics.

 2. Characteristics of Lakes

 2.1 Lake Basin characteristics

Limnological analysis of a lake often requires a detailed knowledge of morphometry, particularly the volume characteristics of the water body. Depth analyses, including areas of sediments and of water strata at various depths, volumes of strata, shoreline characteristics are critical to detailed analysis of physical, biological and chemical analysis. In order to characterize the physical limnology of a lake, a distinction has to be made between a large lake and a small lake. Generally large lakes tend to be deeper than small lakes. Moreover, the ratio of the volume of the water body to its surface area is considerably greater than in small lakes. Table 1 gives morphometric and hydrological differences between Large and small lakes (Imboden,1990).

A lake is divided physically into several zones. The ecological description involves dividing the lake into a littoral, limnetic and profundal zones. The littoral zone is the shallow part of the lake where the light reaches the bottom. The limnetic zone is the offshore part of the lake down to the depth of light penetration. This depth is referred to as the compensation level and describes the point at which photosynthesis and respiration are equally balanced. The term euphotic zone is used to refer to the total of littoral and limnetic zones. The profundal zone includes all the bottom waters below the compensation level. In very shallow lakes and ponds generally the profundal zone is absent.

Lakes are also physically divided by their thermal characteristics. Although this discussion is mainly suitable for temperate lakes, warmer or cooler climates also exhibit thermal characteristics which are basically a subset of these. Since fresh water is most dense at 4^oC, a temperature slightly above the freezing point the lake freezes at the surface in the winter. Except for very shallow lakes, the complete freezing rarely occurs and dense waters remain at the bottom. With the onset of spring the ice melts and surface water begins to warm. During this period, when the vertical temperature gradient is weak wind mixing induces the spring overturn. Continued warming during the summer results warming of surface layers, and wind induced mixing remains in the surface layers, forming typically a three layer structure. The top well-mixed warm layer called epilimnion will be separated with cold bottom hypolimnion waters by a metalimnion or thermocline (Fig. 1). Cooler air temperatures in the fall and winter will lower the epilimnion water temperatures resulting the elimination of thermocline. Mixing of upper and lower layers is then enhanced, resulting in fall overturn. In the tropical belt, although seasonal variations of water temperature are minimum, deeper lakes exhibit partial to strong stratification in the major part of the year. However, hypolimnion rarely forms in the shallow lakes.

 2.3 Heat Balance

One of the most important characteristics of the lake is its thermal structure. The heat content of a water body is of vital importance in the studies of water quality in the lakes. The metabolism, and behavior of aquatic organisms are directly related to the temperature of the water body. Because of high specific heat of water, large volumes of water change temperature slowly. Therefore, large lakes tend to moderate local climates, provide longer growing seasons for aquatic life, and serve an integrated recorders of recent climatic phenomena. Temperature is related to heat content of the water body but does not measure it. The general equation which applies to the heat balance of a water body in a given time interval is 

q_R + q_E + q_L + q_V + q_S + q_B =0

where q_R = net radiation, q_E =latent heat exchange, q_L = sensible heat exchange, q_V = net advective exchange, q_S = change in heat storage and q_B = conductive heat exchange

The net radiation can be measured directly by a net radiometer positioned over the surface of the lake. Alternatively, net radiation may be estimated from the difference between total incoming short-wave radiation, albedo and net long-wave radiation. Latent heat exchange transfer refers to the conduction and convection of heat from the surface of the lake to the air, or vice-versa. Bottom conduction through the sediments is often neglected in the heat balance of small and medium sized lakes. Energy added is considered positive, while energy lost is negative. Over the course of an annual cycle, assuming no climate change, the heat gain is generally equal to heat lost.

 2.4 Water Balance

A water balance for a well-mixed lake can be written as

S = dV/dt = Q_in-Q_out +G +PA_s-EA_s

Where S=Storage (m³/d)

            V=Volume(m³)

            t=time

            Q_in=inflow (m³/d)

            Q_out=outflow(m³/d)

            G=Groundwater flow (m³/d)

            P=Precipitation (m/d)

            E=Evaporation (m/d)

            A_s=Surface area (m²)

In many instances lakes and impoundments (especially large ones) do not experience drastic volume changes for the time periods addressed by water quality models. For such cases water balance equation takes steady state form. Precipitation is measured as the vertical depth in millimeters or inches to which water would accumulate on a level surface in no portion of it is evaporated or runs off, and if frozen precipitation is melted. Evaporation from the water surface is obtained by a simple formula as

E=a (e_s-e_a) (1+bu)

Where e_s is the saturation vapor pressure at the water surface, e_a is saturation vapor pressure of air above the water, u is the wind velocity, and a & b are empirical climatic constants of the lake. Also for small lakes it is easier to measure inflow and outflow, other quantities are generally neglected. Although this simplification is often invoked for expediency, it should be checked for validity.

One important concept useful for water quality studies in the lakes is ‘Residence time’ of water in the lake. If we assume that the precipitation is equal to evaporation in a lake, the sink of water from a lake is measured by the magnitude of the outflow. Then the water residence time is given T_w= V/Q_out, physically speaking this is the time that would be required for the outflow to replace the quantity of water in the lake. Thus it is a measure of lake’s flushing rate. As shown in Table 1, for large lakes since the volume is large compared to outflows, their residence times are high, i.e. they are slow flushers.

 3.0 Water movements

The hydrodynamics of water movements is an integral component of a functional lake system. Physical limnology deals with methods similar to oceanography except that it largely concentrates on the responses of closed basins to applied forces and exchanges of heat. The overall circulation of large lakes is characterized by complicated variations in space and time. With the exception of the circulation induced by hydraulic component of flow in shallow basins wind is the principal source of mechanical energy for water movements in lakes. Except for very large lakes the wind stress is uniform over the lakes. Wind exerts a mean stress (t = C_d r_a U²) or drag on the surface, parallel to the wind direction, and proportional to square of the wind speed (U). The coefficient of proportionality (C_d), known as drag coefficient, varies with several environmental factors. The best known of all water movements influenced by wind are surface waves, however, it is of subordinate interest to most of the water quality considerations because their effect is limited to uppermost strata and therefore they will not take part in the displacement of large water masses. However, in the littoral zone of lakes wave action becomes important because of its role in sedimentation. When the horizontal dimensions of the lakes are sufficiently large, the apparent force due to the rotation of the earth (Coriolis force) has an important effect on the structure of currents and long period waves. The force is proportional to the velocity of the fluid particle and acts at right angles to the velocity.

 3.1 Homogeneous Lakes

Seiches: Standing waves cause much greater water displacements than surface waves and are therefore much more important in physical limnology. Standing waves are a phenomenon occurring in all lakes, but only in large basins we observe periodic rise and fall of the water surface. They are generally known as ‘seiches’.  The seiches are free surface waves, governed by similar dynamics as short, wind generated waves. The principal ingredients in the wave dynamics are acceleration of the water particles and pressure gradients generated by displacement of the free surface and the force of gravity. The speed of these waves is C=ÖgH, where H is local water depth and g is the acceleration due to gravity. In large lakes the earth’s rotation is often important and may influence the motion in the lake. When the natural period of the oscillation is comparable to or greater than inertial period  (12/sin j), the motions are affected by the earth’s rotation. The inertial period is dependent on the latitude (j) of the lake.

Storm surges: A sudden wind will produce not only oscillating seiches, but also cause the water surface to set up or tilt, more or less in opposition to the wind stress, and for the duration of the wind. These changes in water level observed in response to extremely vigorous wind forcing are known as storm surges. The largest change in water level is produced by the sum of storm surge and seiche. Storm surges are largest at the ends of an elongated basin, particularly when the long axis of the basin is aligned with the wind. In low-lying shores such events may cause flooding and increased erosion, with property damages and risk to human lives.

Topographic gyres: The wind drag is transferred from the surface downward by turbulent friction. Because of the closed basins, the transport of water through any cross-section averaged over the period of fundamental seiche is zero. Surface wind-driven flow must be balanced by a subsurface flow that is driven by pressure gradients. Close to the shore, wind drag is experienced all the way to the bottom, and this water is accelerated in the direction of the alongshore component of the wind. The balancing return transport occurs in the middle of the basin. Thus the forced, vertically averaged circulation takes the form of double gyre. The complicated vertical shear maintained during the active wind-forcing soon dies out, leaving this two-gyre motion behind. Within such cross-shore flows, the earth’s rotational force and pressure gradients do not balance and a wave like motion sets up. The two-gyre motion rotates counter-clockwise around the basin in the Northern Hemisphere. These motions are called topographic or vorticity waves. Unlike the influence of topography, the curl of the wind stress generates a single basin-wide gyre that can rotate around the basin, depending on the wind stress.

 3.2 Stratified Lakes

When the lake is stratified, the possibility of vertical displacements of the thermocline as well as those of free surface, introduces more complexity in both wave-like motions and whole-basin circulation.

Coastal Jet:  During strongly stratified regions the force of gravity suppresses turbulence. The vertical transfer of wind-imparted momentum is thus inhibited so much so that the shear stress in the horizontal planes within the thermocline is usually small. This is not true all of the time or everywhere, however, it has been observed in large lakes at least at some distances from shore the momentum of the wind induced coastal current is concentrated in the top, warm portion of the water column above the thermocline. This concentration of momentum in relatively shallow layer results in increased velocities, compared to their depth-averaged values. The region where such concentration was pronounced occupies a band of 5-km width. Their high velocity, shallow depth, and narrow width make it appear to describe the flow structure as ‘coastal jets’ (Csanady, 1982).

Upwelling and downwelling: When wind blows over the stratified lake, the initial transport is confined to the upper layer, which slides over the unperturbed lower layer. At the shores of the lake, accumulations of warm water force the thermocline down (downwelling), and where the warm water moved offshore, the thermocline must rise (upwelling). Figure 2 shows upwelling along the north shore and downwelling along the south shore of Lake Ontario forced by westerly winds.

Given enough time, a steady wind would create a steady setup of the thermocline that would in effect mirror the setup of free surface in such a way that below the  thermocline the pressure gradients set up by the slope of the free surface were exactly cancelled  by those created in the lower layer by the tilt of the thermocline. The strong tendency for the Coriolis force to steer flows in such a way that the pressure gradients are balanced by the Coriolis force limits the upwelling and downwelling zones to a narrow band along the shore line typically within the Rossby radius of deformation. The Rossby radius of deformation  can be defined as the ratio between the typical velocity scale of surface or internal waves, and theCoriolis frequency.

Internal Kelvin waves: When the wind stops, the initial unbalanced state described above relaxes through the mechanism of internal Kelvin waves. Kelvin waves propagate alongshore in a counter-clockwise direction in the Northern Hemisphere. Internal Kelvin waves are confined to a few kilometers from the shore, and with no motion in the perpendicular direction to the coast. The near surface currents that moved in the downwind direction during the active wind phase now reverses during the propagation of these waves.

Near-Inertial motions: During the stratified season in the offshore areas of the lake, currents exhibit clockwise rotary motions close to the inertial period (Fig. 3). Similar motions occur in the oceans, anywhere the water can move horizontally without the hindrance from the shore. The main features may be explained in terms of balance between the Coriolis force and the centrifugal force. A sudden wind impulse lasting less than half the inertial period is favourable to the creation of inertial motions. Observations also showed that similar motions in the deeper layers where the direction is generally opposite to that of surface oscillations. These motions are called Poincare waves, which are similar to internal seiches in small lakes. The currents are accompanied by vertical oscillations of thermocline at the wave period. These waves are hybrid between pure inertial motion described above and gravity waves; the current vector rotates in clockwise direction at a frequency close to but usually larger than local inertial frequency.

Inflow and Outflow currents: Currents brought about by inflow and outflow of water is of special importance in lakes on larger rivers. Hypolimnetic water is usually replenished by a cold water inflow. To illustrate these consider the mixing of a large river plume. The receiving water circulation, strength of the river plume, wind direction, the formation of the basin and the effect of the earth’s rotation, fixes the path this inflowing current takes in the lake. The outflow normally draws off water from the surface and the strata immediately below it, and thus brings about a considerable loss of heat in small and medium lakes. This withdrawl of heat, and thus also the surface temperature of the lake, is influenced by the form and profile of the outlet. It the outlet is wide and shallow the loss is greater than when it is narrow and deep. For small outflows and/or strong stratification the water is removed by a thin layer adjacent to the level of outflow which is called as selective withdrawal.

Vertical convection currents: Apart from wind or river induced circulation, currents can also be generated internally due to stratification effects. As we have seen earlier in spring and fall overturns, these currents draw their energy from changes in density due to surface cooling and heating. Differential cooling and heating is also very important in shallow lakes and may be responsible for flushing of littoral waters.

 4.0 Mixing

Mixing processes in lakes cover a wide spectrum of different time and length scales. At the small end of these scales, mixing processes are similar in oceans and lakes. With increasing size and duration of the mixing structure the different dimensions of the water bodies become more apparent. Typically horizontal exchange of heat, energy and momentum occur at scales generally much larger than vertical exchanges, given the large horizontal lengths of lakes compared to their depths. This has prompted many researchers to de-couple horizontal transports from the vertical ones, even though horizontal and vertical processes interact. Spectral analysis is the method commonly used to isolate the various phenomena. For instance, time series of currents or temperature measured at a fixed station in lakes can be decomposed by Fourier transformation into modes of different frequencies (Fig. 4 ).

In the inertial sub-range the similarity theory predicts that the turbulent kinetic-energy spectrum E(k) is given by the familiar - 5/3 power law , where c is a universal dimensionless constant; c is the rate of dissipation of turbulent kinetic energy and k is the wave number. We assume that turbulent eddies larger than the size of the diffusing cloud does not contribute much to the diffusion process.  Furthermore, if we designate a length scale i =  k^-1 to the eddies responsible for the diffusion of the cloud, then for a point source initially released into a turbulent medium consisting of a spectrum of eddies of several sizes, the turbulent kinetic energy available for diffusion of the cloud

would be . Combining the above two equations the turbulent velocity

associated with length scale, l, is given by: Following mixing length arguments an effective horizontal diffusivity of the diffusion process can be defined by: , which is the Richardson's 4/3 power law of diffusion.  The physical meaning of the Richardson's 4/3 power law is that the inertial sub-range eddies are active and the diffusion process is characterized by two parameters, c, the rate of turbulent energy dissipation, and, 1, the length scale of eddies. Experimental diffusion data from the oceanic and aquatic environment validate the Richardson's 4/3 power law of diffusion quite well. The dependence of the effective diffusivity on the length scale provides useful guidelines for modelling of practical diffusion problems in the natural environment.

As an example typical sizes characterized by energy and momentum fluxes in large lakes are given in Table 2.

Many mixing processes in lakes are of singular nature, this means that they are triggered by some external or internal force and then evolve along a characteristic pathway determined by the hydrodynamic laws. For example the phenomena that was described earlier about storms producing upwelling and downwelling at opposite shores, produces mixing through the subsequent relaxation through the generation of internal waves and smaller scale processes. Boundary mixing is very important mechanism for mixing in small lakes. An effective vertical transport is realized by vigorous mixing at the boundary fluid intruding gravitationally into the hypolimnion. Turbulence is also generated by a variety of internal wave instability and interactions (Fisher et al.,1979). Since internal waves are generated at the underside of the thermocline and at lake boundaries, energy may be transferred from wind through the thermocline to the internal waves which then interact with each other in a variety of possible instability mechanisms to produce local mixing event.

There exists a variety of other less spectacular events. Many of them are connected to density induced mixing. For example river-induced currents may be significant in some lakes for the exchange of water from below the thermocline. The river plume often enlarged in volume by water entrained from the lake surface, push hyplomnic water upwards, thus adding to vertical mixing. The daily interaction between meteorological forcing and mixing at the lake surface also belongs to the category of events. The diurnal cycles of heating and cooling cause a complicated temporal and spatial variation of temperature distribution in the mixed layer. Langmuir circulation cells are often referred as one important mechanism for mixing in the upper mixed layer.

 References

Csanady, G.T. (1982) Circulation in the coastal ocean, D. Reidal Publishing company, Boston, pp. 279.

 Imboden, D.M. (1990) Mixing and transport in Lakes: Mechanisms and ecological relevance, Large Lakes: Ecological structure and Function (Eds: M.M. Tilzer and C. Serruya).

 Fisher, H.B. et al. (1979) Mixing in inland and coastal waters, Academic Press, New York,150-222.

Fig. 1: Vertical thermal structure in a large temperate lake.

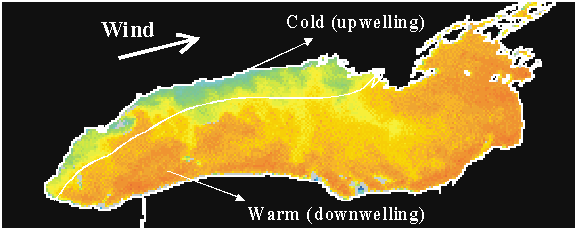
Fig. 2: Satellite picture showing upwelling along the north shore and downwelling along the south shore of Lake Ontario during a westerly wind event.

Fig. 3: Progressive vector diagram showing inertial oscillations.

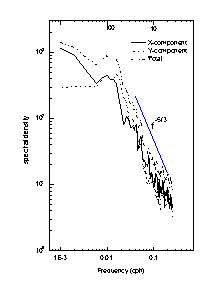
Fig. 4: Total and two components of current spectra.