INTRODUCTION:

The unsaturated zone sometimes called the Vadose Zone between the ground surface and the water table includes the precipitation that reaches the land surface and artificial water applications such as irrigation, surface runoff, stream flow, lakes and artificial impoundment. The rainfall may infiltrate and some of the surface water may percolate through the unsaturated zone. Many constituents present in the surface water eventually find their way into the groundwater through the unsaturated zone. Accidental spills of chemicals, application of fertilizers and pesticides on the land surface, leaks from gasoline storage tanks, septic tank drainage, and leaching from landfills are examples of anthropogenic activities that contribute to the leaching of contaminants through the unsaturated zone into the groundwater. The source activities, primarily responsible for release of pollutants into the subsurface, cannot be eliminated. Hence, the goal of groundwater protection efforts must necessarily be the control and management of these sources to ensure the released pollutants are sufficiently attenuated within the subsurface to prevent significant impairment of groundwater quality at points of withdrawal or discharge. This goal can be effectively achieved only if control and management options are based on definitive knowledge of the transport and fate of pollutants in the subsurface environment.

In the past, several attempts have been made to address this problem (Herbert et al., 1963; Tej Ram Nayak and Lakshminarayana, 1990; Volker and Guvanasen, 1979). Computer methods for simulating such movements have also been developed (Shamir and Harleman, 1967; Oster et al., 1970; Amithirigala et al., 1999; Bruch et. al., 1967; Bresler et al., 1973a, 1979). In many of their works, the solute was assumed to be inert with respect to its environment, so that interaction with the soil matrix was ignored. In addition, all these studies were limited to situations in which the soil or the porous material was completely saturated with solution or has constant unsaturated water content. Warrick et al., (1971) presented a numerical simulation technique to approximate the displacement of a non-interacting solute during infiltration. To simplify their solution procedure, they assume that the time required to establish a reasonably steady rate of intake is small compared with the overall infiltration time.

The objective of this paper is to describe the simultaneous transport of solutes through soil profiles during transient flow conditions. The combined effects of convection and mechanical dispersion are investigated and analyzed. The results are compared with simplified analytical solutions and with observed data. Typical results are presented to show their effects on the dispersion coefficients and solute profiles.

MATHEMATICAL MODEL

In dealing with the problem of simultaneous transfer of solute and water, one usually assumes that convection and diffusion govern the transport of the solute. In general, molecular diffusion takes place together with the convective transport, and each process contributes to the final dispersion of the solute. It is generally assumed that macroscopic transport by convection must take into account the average flow velocity as well as the mechanical or hydrodynamic dispersion. Solutes are transported by convection at the average velocity of the solution, and in addition they are dispersed about the mean position of the front.

Combining their mathematical expressions to obtain the combined effect of diffusion and convection is,

FINITE DIFFERENCE SOLUTION

The finite difference solution may cause considerable smearing of the concentration profiles, a phenomenon known as numerical dispersion. This numerical dispersion may limit the applicability of the solution. Its value usually depends on the flow velocities as well as the space and time increments. Therefore, the space-time continuum (z, t) is subdivided into a network of rectangular cells.

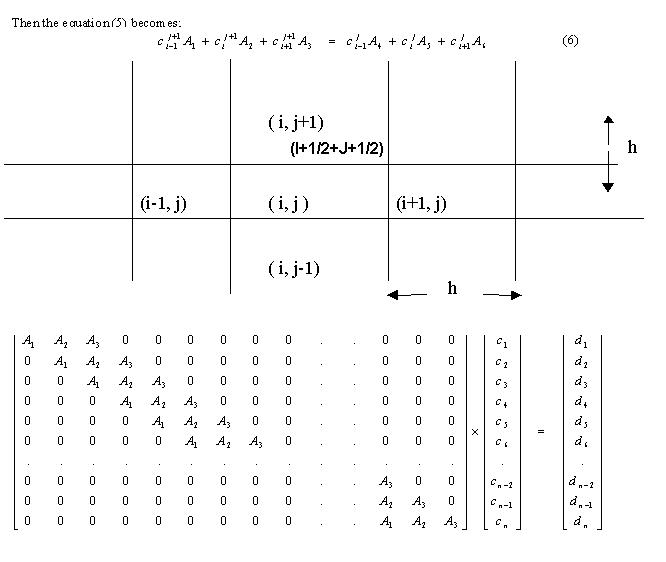
RESULTS AND DISCUSSIONS

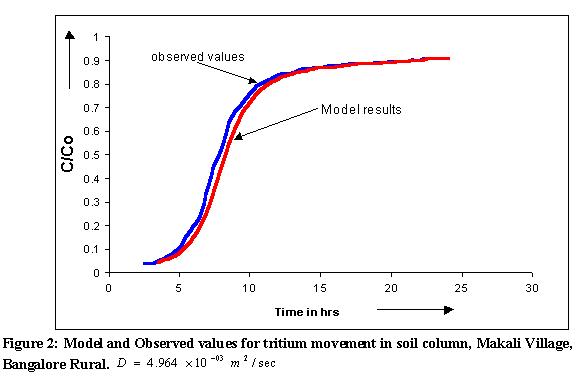
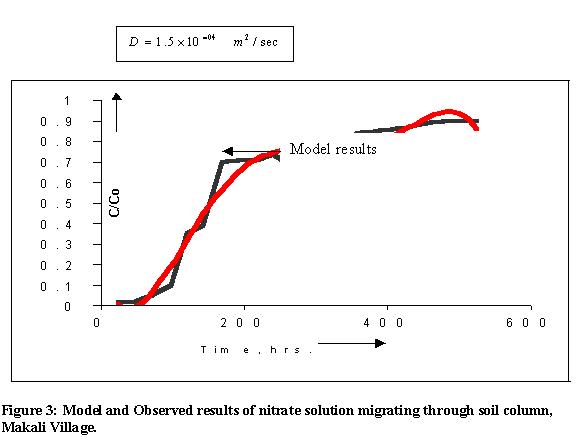
The flow velocities and longitudinal dispersion coefficient are determined experimentally by allowing the solute to pass through the soil columns. The undisturbed soil columns were collected from Mallasandra (Chickballapur) and Makali village (Bangalore Rural). Basak and Murthy (1978, 1979) have attempted to provide a useful and unique method for quick determination of the hydrodynamic dispersion coefficients from soil column experimental data. The percolated effluents from soil columns were collected and the concentrations of solutes (tritium and nitrates) were measured (Ranganna, et al 2000).

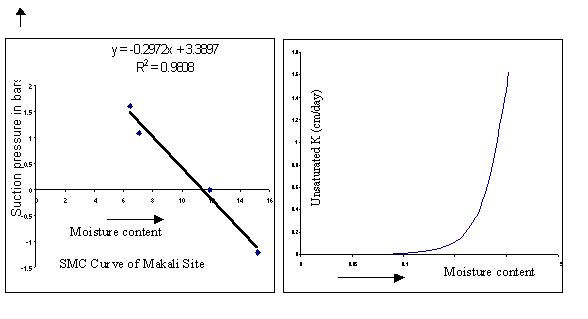
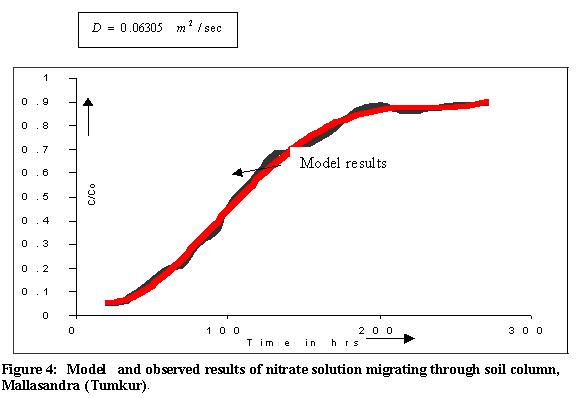
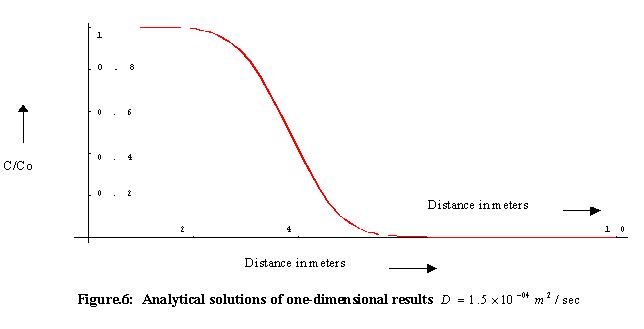
Three soil samples from Thirnahally of Mallasandra and Makali village were collected. Suction pressure for various corresponding moisture contents was measured in the laboratory. The soil moisture curves were plotted. Using the resulting SMC relationship, the unsaturated hydraulic conductivity K (q) for these sites was developed. Using K (q)-q relationship, the unsaturated flow velocity is computed. Figure.1. shows the SMC curves, K (q)-q relationship and Break through curve observed after passing the tritium through soil column of Makali village. Using the diffusion coefficients and flow velocities computed from the soil column experiments, the equation (6) is solved and the results plotted. Figures 1 to 6 show the results obtained from the finite difference solution for different sites and diffusion coefficients and observed values. An analytical solution for one-dimensional case has also been developed to check the accuracy of the finite difference solutions.

The finite difference expressions developed herein should prove helpful in making quantitative predictions on the possible contamination of groundwater supplies resulting from seepage of high salt concentrations in drainage ditches, canals and streams and from groundwater movement through buried wastes. The finite difference solution may be useful for verifying the numerical accuracy of more comprehensive finite element solutions and finite volume solution to the transport equations as well as for investigating some aspect of the transport process in porous media that has a distance dependent dispersion function of the described form.

REFERENCES:

Address:

1.) U. V. C. E.,
Jnanabharathi,
Bangalore University,
Bangalore-560 056.
2.) U G C-D S A Center in Fluid mechanics,
Dept. of Mathematics,
Bangalore University,
Central College Campus,
B'lore - 560 001.