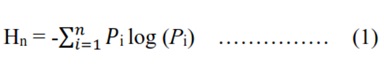|
Method
Preprocessing: This involved geo-referencing of data, done with the help of known location points (compiled from the Survey of India topographic maps and also from field using pre-calibrated GPS – Global Positioning System). Remote sensing data were cropped corresponding to study regions with ten km buffer. Co-ordinates of known locations such as road intersections, edges of huge permanent structures like dams, bridges etc. were compiled using GPS and online high resolution data (Google-earth) at inaccessible places. Further, resampling was performed to maintain the spatial resolution uniformity across temporal remote sensing data. Histogram equalization was performed wherever enhancement was necessary to maintain the dynamic range. Landsat and IRS LISS-III images were coregistered to WGS 1984 and UTM zone 44.
Land cover analysis: Land cover refers to the original earth surface features that are formed naturally in the form of vegetation, water body, etc. (Ramachandra et. al., 2013). Land cover analysis helps to understand the changes of the vegetation cover over the study area at different time periods. It is obtained by performing normalized difference vegetation index (NDVI). NDVI value ranges from -1 to +1. Values consisting of -0.1 and below indicates soil, barren land, rocky outcrops, built up/urban cover, whereas water bodies are indicated by zero values. Low density vegetation is indicated in the range +0.1 to +0.3 while high density vegetation or thick forest canopy is given in the range +0.6 to +0.8.
Land use analysis: Land use analysis starts withgeneration of false colour composite (FCC)of 3 bands(Green, Red and NIR). Creation of FCC directly helpsin identifying heterogeneous patches in the landscape(Ramachandra et al., 2014). Training polygons aredigitized based on the distinguishable heterogeneousfeatures in FCC, covering at least 15% and uniformly distributed across the entire study area. These polygons and its coordinates with GPS and attribute information is compiled with respect to corresponding land use type (ground truth data). Training polygons were supplemented with the data available at Google earth for classification. 60% of these training polygons were used for classification purpose while the rest 40% for validation and accuracy assessment. Supervised Gaussian maximum likelihood classification (GMLC) was employed to assess quantitatively land uses in the region. GMLC algorithm considers cost functions as well as probability density functions and proved to be efficient among other classifiers (Duda et al., 2000). It evaluates both variance and co-variance of the category while classifying an unknown pixel (Lillesand et al., 2012). Land use classification under four categories (table 3) using GRASS.
| Category |
Features involved |
| Builtup |
Houses, buildings, road features, paved surfaces etc. |
| Vegetation |
Trees, gardens and forest |
| Water body |
Sea, lakes, tanks, river and estuaries |
| Others |
Fallow/barren land, open fields, quarry site, dry river/lake basin etc. |
Table 3: Land use categories
Accuracy assessment: Possible errors during spectral classification are assessed by a set of reference pixels collected by ground data collection. Based on the reference pixels, statistical assessment of classifier performance including confusion matrix, kappa (κ) statistics and producer and user's accuracies were calculated. These accuracies relate solely to the performance of spectral classification. Entire method followed has been summarized in figure 2.
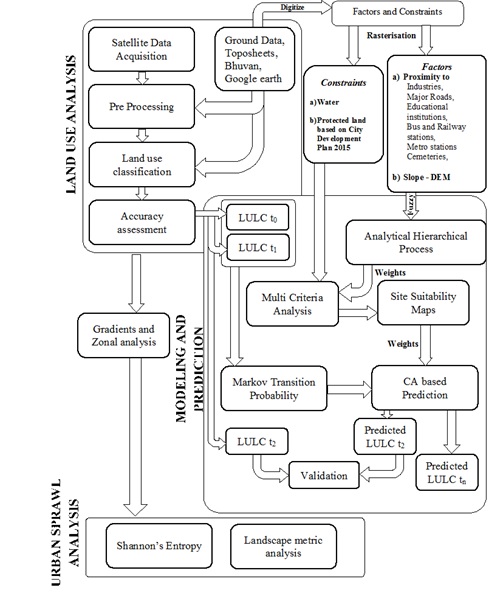
Figure 2: Method adopted to understand, quantify and model urban growth
4.1. Density gradient and zonal analysis:
Earlier investigations of spatial patterns of urbanisation were restricted to political boundaries (Taubenbock et al., 2009; Deng et al., 2009; Sadhana et al., 2011). In order to understand the growth at local levels, specific to neighborhood, the entire study area was divided based on directions into four zones (i.e. North East (NE), North West (NW), South East (SE) and South West (SW) and concentric circle with the central business district as centroid and incrementing radii of 1km. The zone wise concentric circle based analyses was performed helped to interpret, quantify and visualize forms of urban sprawl pattern (low density, ribbon, leaf-frog development) and agents responsible in urbanization at local levels spatially (Ramachandra et al., 2014b).
4.2. Spatial patter analysis:
Shannon's entropy (Hn) is computed (equation 1) to determine whether the growth of urban areas is compact or dispersed growth. Dispersed growth is also known as ‘urban sprawl’ This analyses gives a better understanding of degree of spatial concentration or dispersion of geographical variables among “n” concentric circles across four direction zones. Also, the regions undergoing sprawl needs decision makers’ attention to provide appropriate infrastructure and adequate basic amenities.
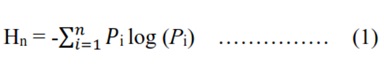 where, Pi is the proportion of the built-up in the ith concentric circle. Shannon’s Entropy, values ranges from 0 to log n. 0 if the distribution is maximally concentrated whereas log n indicates sprawl.
where, Pi is the proportion of the built-up in the ith concentric circle. Shannon’s Entropy, values ranges from 0 to log n. 0 if the distribution is maximally concentrated whereas log n indicates sprawl.
4.3. Spatial metrics:
Metrics pertaining to spatial heterogeneity of patches, classes of patches, or entire landscape mosaics of a geographic area (O’Neill et al., 1988, Herold et al., 2005) give quantitative description based on the composition and configuration of the urban pixels in a landscape. Spatial metrics were computed for urban class through FRAGSTATS (McGarigal and Marks, 1995) for each zone and density gradients. Table 4 lists prioritized (based on our earlier work (Ramachandra et al., 2012, Ramachandra et al., 2015) six metrics to characterize urban growth.
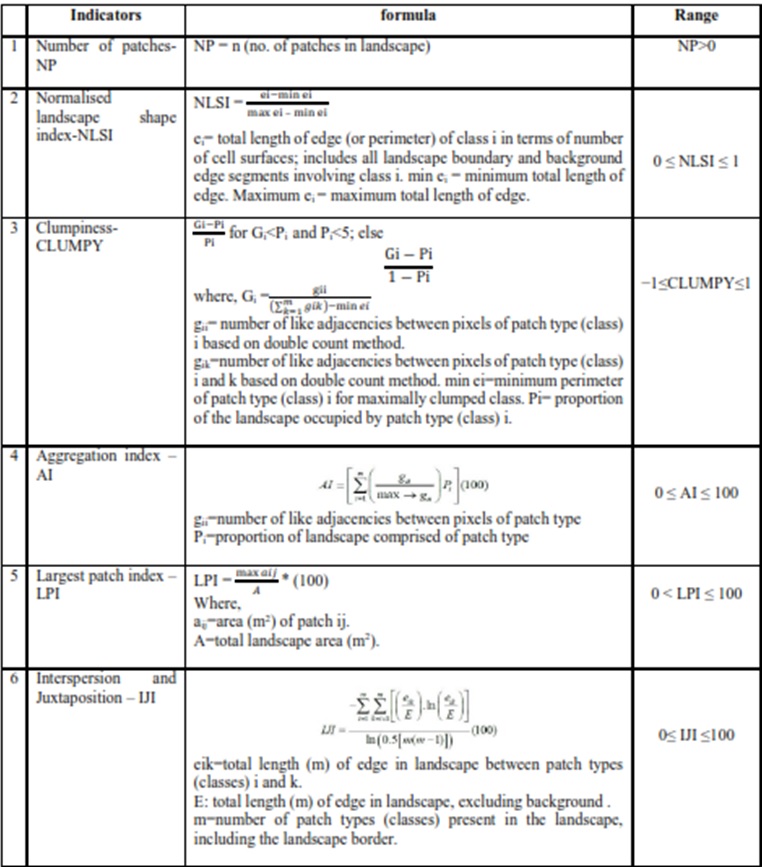 Table 4: Spatial metrics used
Table 4: Spatial metrics used
4.4. Modelling:
Urban growth during 2025 is predicted considering agents with constraints (listed in table 5) and base layers of historical land uses (based on the classified temporal remote sensing data). Data values were normalized (between 0 and 255) through fuzzyfication wherein 255 indicates maximum probability of land use changes. Fuzzy outputs thus derived are then taken as inputs to AHP for different factors into a matrix form to assign weights. Each factor is compared with another in pair wise comparison followed by enumeration of consistency ratio which are to be<0.1 for the consistency matrix to be acceptable (Saaty, 1980).
Constraints were assigned considering city development plan (CDP), Digital elevation model and slope data. Drainage lines were delineated using ASTER DEM and a buffer of 30m from drains were assigned constraint to restrict development as per the guidelines of the regional metropolitan development authority. Constraints and factors were fed to multi criteria evaluation (MCE) (Table 5). The MCE approach combines various criteria into a single index that indicates the site suitability of specific land use of each location in the study area. Markovian transition estimator provided bi-temporal land use data to estimate transition and predict future likely land uses. Probability distribution map was developed through Markov process. First-order Markov model based on probability distribution over next state of the current cell that is assumed to only depend on current state. CA was used to obtain a spatial context and distribution map. Transition suitability areas and matrix, iterations to be performed and filter stipulations are carried out by CA coupled with Markov chain to predict future land use. Validation of predicated data was done by comparing reference (classified) image versus the predicted image for the same year (in this case 2014). Various kappa indices of agreement and related statistics were calculated. Further, Land use is predicted for 2025.
| Agents |
Industries, proximities to roads, railway stations, metro stations, educational institutes, religious places etc. |
| Constraints |
Drainage lines, slope, water bodies, regulated regions for non-development, Protected areas, coastal regulated areas, sensitive regions in a catchment, etc. |
Table 5: Agents and constraints considered for modelling
|