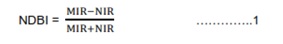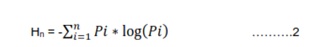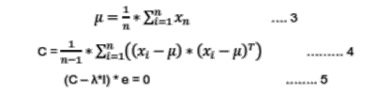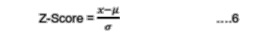|
Data Analysis
5.1 Normalised Difference Built-up Index (NDBI)
NDBI is useful to map the urban built-up regions as paved surfaces (such as built-up land, roads, etc.) have relatively higher reflectance in MIR (1.55 to 1.75μm) and NIR (0.76 to 0.90μm) wavelengths in comparison with other surface features of the earth (Li and Liu, 2008, Chen et al., 2013). NDBI is computed using the equation 1 and values range from -1 to +1, and higher NDBI values indicate dense built-up region.
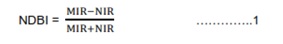
5.2 Land use
To understand the temporal dynamics of the landscape, land use analyses were done using Gaussian maximum likelihood classifier (GMLC). Classified land uses include built up, water, agriculture andothers. Table 1 lists grouping of sub classes for the respective land use category. Analysis involvedgeneration of False Color Composite (FCC) using the data of NIR, Red and Green bands that helps inthe identification of heterogeneous patches of landscape (Ramachandra et al., 2013a), trainingpolygons were collected from these select heterogeneous patches covering at least 15% of the studyregion. Attribute data of these training polygons were collected from field with the help of GPS in additionto Google earth (http://earth.google.com) and Bhuvan (http://bhuvan.nrsc.gov.in). These training data(60%) were used to classify and the remaining were used to validate the classified land use.Classification was carried out using the Gaussian Maximum Likelihood Classifier (Duda et al., 2005,Ramachandra et al., 2013b) based on the probability density function considering the mean andvariance. The classification was carried out using the open source GRASS (Geographic Resource Analysis Support System, http://ces.iisc.ac.in/grass) GIS.
Evaluation of the performance of classifier is done through accuracy assessment techniques. Accuracy assessment (Ramachandra et al., 2013b, Bharath and Ramachandra et al., 2013) decides the quality of the information derived from remotely sensed data. The accuracy assessment is the process of measuring the spectral classification inaccuracies by a set of reference pixels. These test samples are then used to create error matrix (also referred as confusion matrix), kappa (κ) statistics and producer's and user's accuracies to assess the classification accuracies. Kappa is an accuracy statistic (Congalton et al 1983, Ramachandra et al., 2102c) that permits us to compare two or more matrices and weighs cells in error matrix according to the magnitude of misclassification.
| Land use Class |
Land uses included in the class |
| Urban |
This category includes residential area, industrial area, and alpaved surfaces and mixed pixels having built up area. |
| Water bodies |
Tanks, Lakes, Reservoirs. |
| Vegetation |
Forest, Cropland, Nurseries. |
| Others |
Rocks, quarry pits, open ground at building sites, kaccha roads. |
Table 1. Land use categories
5.3 Gradient Analysis
Each study region (metropolitan mega cities with 10 km buffer) was divided into four zones (NE, NW, SE, and SW based on directions) and concentric circles of incrementing one km radii (from the center of city) to visualize the spatial patterns of changes at neighborhood level (Ramachandra et al., et al 2011). Direction based gradient analyses aids in identifying/understanding the causal factors, degree and rate of urbanization at local levels in each gradient. Shannon entropy indicator of urban sprawl is used to understand the spatial extent of urbanization (compact growth or fragmented growth). Shannon entropy (H n) (Lata et al 2013, Sudhira et al 2004) was calculated across directions with respect to the gradients (“n” regions corresponding to concentric circles) for each city. Shannon entropy is given by equation 2.
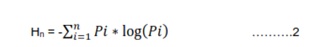 Where Pi is the proportion of the built-up in the ithconcentric circle and n is the number of circles/local regions in the particular direction. Shannon’s Entropy values ranges from zero (maximally concentrated) to log n (dispersed growth).
Where Pi is the proportion of the built-up in the ithconcentric circle and n is the number of circles/local regions in the particular direction. Shannon’s Entropy values ranges from zero (maximally concentrated) to log n (dispersed growth).
5.4 Spatial Metrics Analysis
Spatial metrics provides a quantitative description and configuration of the urban land scape (Ramachandra et al., 2012b, Ramachandra et al., 2013c). The metrics were calculated for each gradient using FRAGSTATS (McGarigal and Marks in 1995). The metrics that were calculated includes CLUMPY, IJI, LPI, LSI, NLSI, NP, PD, PLAND and the description of these metrics are given in Table 2.
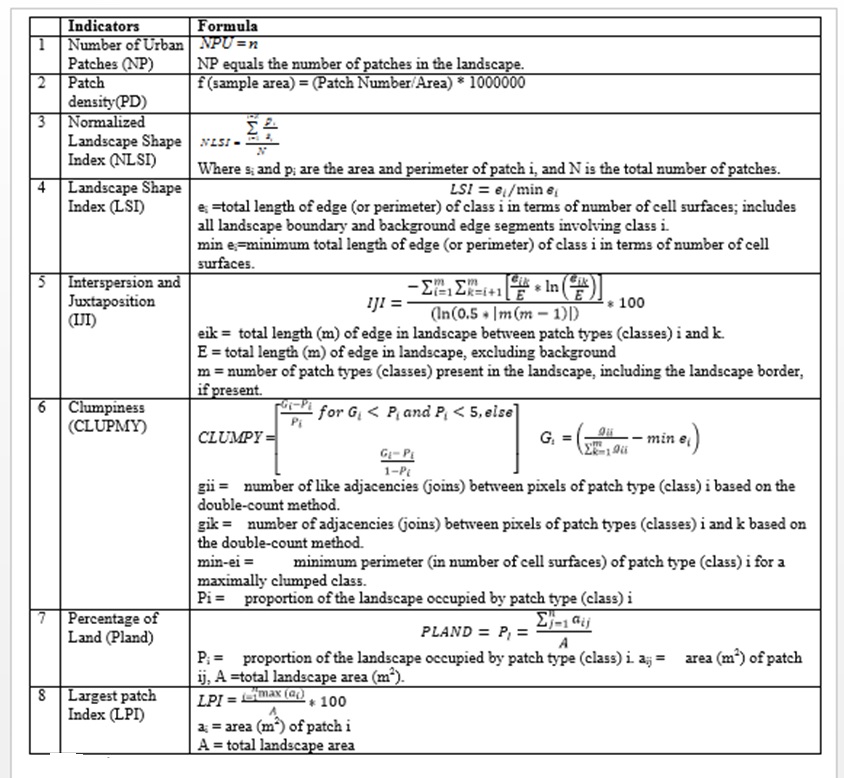 Table 2. Landscape metrics analysed
Table 2. Landscape metrics analysed
5.5 Principal Component Analysis (PCA)
Principal component analysis was carried out to explore the overall spatial patterns of intra and inter region variation in urban form considering landscape metrics computed for each gradient corresponding to four zones of cities (Ramachandra et al., 2015b, Narumasa et al 2013, Madugundu 2014). PCA computes the sample mean ‘μ’ and covariance ‘C’of all the parameters ‘n’and their measurements ‘m’ respectively (equations 3 and 4). The covariance matrix is used to compute the Eigen value ‘λ’ and Eigen vectors ‘e’ (equation 5). These Eigen vectors represent the principal components of every measurement, the number of Eigen vectors generated would be equal to the number of parameters. The Principal components are then prioritised based on the Eigen vectors.
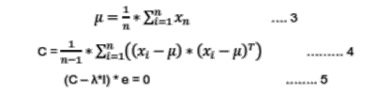 The priorotised landscape metrics such as CLUMPY, IJI, LPI, LSI, NLSI, NP, PD, Pland were used as the components and the measurements were made/considered for every city across gradients along the 4 directions for each decade. These landscape indices (measurements) were normalized using ZScores (equation 6) prior to Principal Component Analysis.
The priorotised landscape metrics such as CLUMPY, IJI, LPI, LSI, NLSI, NP, PD, Pland were used as the components and the measurements were made/considered for every city across gradients along the 4 directions for each decade. These landscape indices (measurements) were normalized using ZScores (equation 6) prior to Principal Component Analysis.
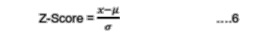 The scatter plot of Principal components that explains maximum variation of data (example PCA1 versus PCA2) helped in eliciting the urbanization patterns across various gradients, directions and cities. This analysis was helpful to bring out the systematic similarities and differences between the gradients across cities
The scatter plot of Principal components that explains maximum variation of data (example PCA1 versus PCA2) helped in eliciting the urbanization patterns across various gradients, directions and cities. This analysis was helpful to bring out the systematic similarities and differences between the gradients across cities
|