The complexity of a dynamic phenomenon such as urban sprawl could be understood with the analyses of land use changes, sprawl pattern and computation of sprawl indicator index. As a prelude to this analysis, GIS base layers such as, road network and the administrative boundaries from the toposheets as shown in Table 1 were created. The highway passing between the cities was digitised separately and a buffer region of 4 km around this was created. This buffer region is created to demarcate the study region around the road. Following this, land cover analyses were done using remote sensing data. 

The growth of urban sprawl over a period of three decades was determined by computing the area of all the settlements from toposheets of 1972 and comparing it with the area obtained from the classified satellite imagery for the built-up area. The detailed methodology followed is depicted in the flow chart (Figure 4). The toposheets (Table 1) in digital format were scanned and then geo-registered. The area under built-up (for 1972) was added to this attribute database after digitisation of the toposheets for the built-up feature for the study area. 

Urban sprawl is a process, which can affect even the smallest of villages; hence each and every village was analysed. Attribute information like village name, taluk it belongs to, population density, distance to the cities, were extracted from census books of 1971 & 1981 and were added to the database. The area under built-up (for 1972) was computed and appended to this attribute database. 

The multispectral IRS – LISS III satellite imagery procured from National Remote Sensing Agency (NRSA), Hyderabad, India, was used for the analysis using IDRISI 32 (http://www.clarklabs.org). The image analyses included bands extraction, restoration, classification, and enhancement. Band extraction was done initially through a programme written in C++ and subsequently IDRISI 32 was used for image analyses. Geo-registered LISS III data obtained from NRSA (bands 2, 3 and 4 corresponding to G, R, MIR) were geo-corrected using resampling techniques. This is done with the help of known points on the Survey of India toposheets or / and ground control points (GCPs) using GPS. The data acquired in bands -Green, Red and Near Infrared were used to generate a False Colour Composite (FCC). To create the composite image from three input bands, each of the three bands is stretched to 6 levels (6 * 6 * 6 = 216). The composite image consists of colour indices where each index = Green + (Red * 6) + (Near Infrared * 36) assuming a range from 0-5 on each of the three bands. For example, a pixel value of 3, 5, 1 respectively for the three bands, Green, Red and Near Infrared would have an index of 3 + (5 * 6) + (1 * 36) = 69. The 256 Colour Composite palette colours correspond to the mix of Green, Red and Near Infrared in the stretched images. In the composite image, heterogeneous patches were identified and the corresponding attribute data was collected using GPS (Global Positioning System).   

Corresponding to the training data, signature files with attribute information were created. For the image classification supervised classification by the Maximum Likelihood Classifier (MLC) or Gaussian classifier was employed.  Area under built-up theme was recognised and extracted from the imagery and the area for 1998-99 was computed. Further, by overlaying village boundaries, villagewise built-up area was calculated. 

The percentage of an area covered by impervious surfaces such as asphalt and concrete is a straightforward measure of development (Barnes et al, 2001). It can be safely considered that developed areas have greater proportions of impervious surfaces, i.e. the built-up areas as compared to the lesser-developed areas. Further, the population in the region also influences sprawl. The proportion of the total population in a region to the total built-up of the region is a measure of quantifying sprawl.  

Considering the built-up area as a potential and fairly accurate parameter of urban sprawl has resulted in making considerable hypothesis on this phenomenon. Since the sprawl is characterised by an increase in the built-up area along the urban and rural fringe, this attribute gives considerable information for understanding the behaviour of such sprawls. This is also influenced by parameters such as, population density, population growth rate, etc.  

Pattern recognition helps in finding meaningful patterns in data, which can be extracted through classification. Digital image processing through spectral pattern recognition wherein the spectral characteristics of all pixels in an image were analysed. By spatially enhancing an image, pattern recognition can also be performed by visual interpretation. 

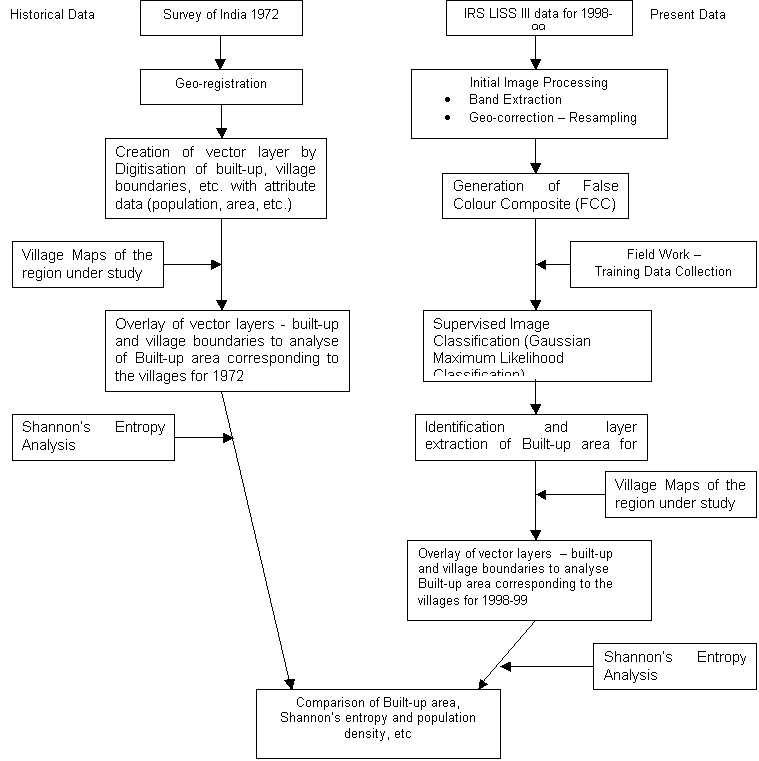
 Figure 4: Flow Chart of Methodology of Analysis of Urban Growth

Characterising pattern involves detecting them, quantifying with appropriate scales and summarising it statistically. The agents of pattern formation include the physical abiotic component, demographic responses to this component, and disturbance regimes overlaid on these. An interest in landscape dynamics necessarily invokes models of some sort because landscapes are large and they change over timescales that are difficult to embrace empirically. Spatial heterogeneity matters to populations, communities, and ecosystems and these are the essentials of conservation and ecosystem management. Various landscape metrics were applied to analyse the built-up theme for the current study. The landscape pattern metrics are used in studying forest patches (Trani and Giles, 1999; Civco, et al., 2002). The landscape metrics applied to analyse the built-up theme for the current study is discussed next. 

There are scores of metrics now available to describe landscape pattern, but there are still only two major components--composition and structure, and only a few aspects of each of these. Most of the indices are correlated among themselves, because there are only a few primary measurements that can be made from patches (patch type, area, edge, and neighbour type), and all metrics are then derived from these primary measures.  

Need for computing indices of landscape pattern:

1. For comparative purposes, to summarise the differences between or among study areas or landscapes

2. To infer underlying agents of pattern formation, that is, as an exploratory analysis that is a precursor to more strategic hypothesis testing.

The latter goal is fundamental to landscape ecology if not ecology in general.  Also, the task of attributing causal mechanism (process) to observed pattern is more daunting than expected. Some of the common objectives of landscape studies are: 

1. To detect and quantify pattern in the spatial heterogeneity of landscapes;

2. To develop and test a set of indices that capture important aspects of landscape pattern;

3. To relate the indices with ecological phenomena;

4. To link small-scale ecological information (i.e., field data) with pattern at the landscape level.

The Shannon’s entropy (Yeh and Li, 2001) was computed to detect and quantify the urban sprawl phenomenon. The Shannon’s entropy, Hn is given by,

Hn = - S Pi log_e (Pi)                             ………………. 1

where;

Pi = Proportion of the variable in the i^th zone (i.e. proportion of built up area in each village)

n = Total number of zones (i.e. number of villages in the region) 

The value of entropy ranges from 0 to log n. Value of 0 indicates that the distribution is very compact, while values closer to log n reveal that the distribution is very dispersed. Higher values of entropy indicate the occurrence of sprawl (refer annexure for computation details). 

Patchiness or NDC (Number of Different Classes) is the measurement of the density of patches of all types or number of clusters within the n*n window. In other words, it is a measurement of the number of polygons over a particular area. The greater the patchiness, the more heterogeneous the landscape is (Murphy 1985). 

In order to compute the map density initially the class frequency of the required feature is computed. The class frequency is the number of times a specified characteristic value occurs within a kernel. The kernel can be of 3 x 3, 5 x 5, or 7 x 7. The kernel is centred on each built-up pixel of the classified image in the manner of a moving window. A new value for the centre pixel is assigned to the corresponding position of the output image. For the value to be counted it must fall within one of the positions marked by a 1 in the selected kernel: 3 x 3    

1          1          1

1          1          1

1          1          1

The kernel size selected depends upon the scale of the information to be derived.