

|
Catchment Possibilities and Choice of Reservoir Types Calculation of Rainwater Volume and Choice of Reservoirs |


|
Catchment Possibilities and Choice of Reservoir Types Calculation of Rainwater Volume and Choice of Reservoirs |
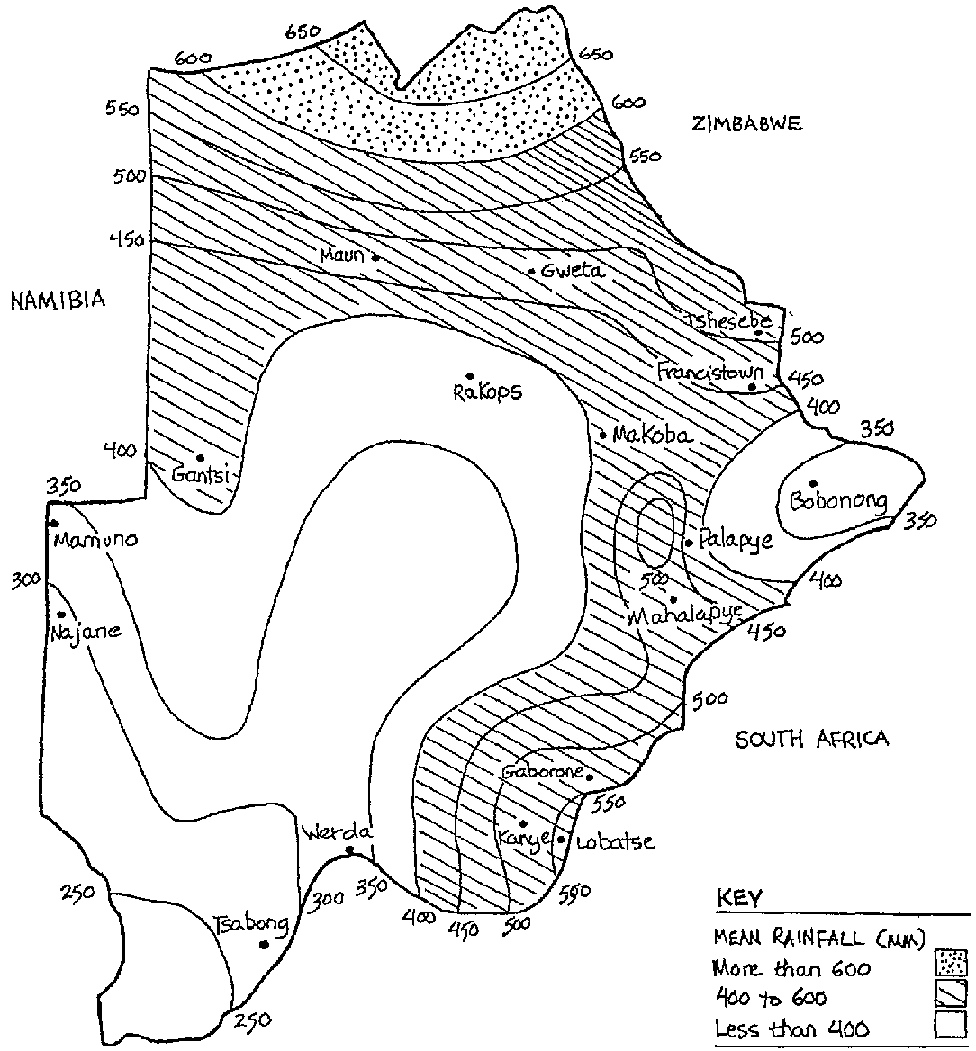
To calculate the rainwater amount which can be harvested, the mean annual rainfall figure is commonly used. Mean annual is the statistical average calculated on the basis of measured rainfall over many years. It has to be understood that there is no guarantee that the calculated amount will be achieved, but there is a 95% likelihood that this amount can be expected. This near certainty diminishes to a probability if the rainfall pattern in a given area differs substantially. This is quite common in countries with drought periods. It can happen that the mean annual cannot be expected. It can certainly happen the other way round that considerably more rain falls than the mean annual. This makes the calculation of the storage capacity rather difficult. However, the mean annual is generally accepted as the basis. The size of, storage capacity chosen can be based on the mean annual, but should be greater if funds allow. Some countries provide maps where the mean annual rainfall is indicated along the line of occurrence. Fig. 2.1 shows the rainfall in Botswana; each line is marked with a figure giving the precipitation. The mean annual in a given area between two lines ranges from the lower amount, for instance 400 mm, to the higher average of 450 mm. For example the mean annual rainfall in Gweta is between 450 and 500 mm.
As an example let us consider a roof of 120 m² in an area with mean annual rainfall of 450 mm. We assume that less than 100% of the calculated amount of water will be collected. This is due to unavoidable small leakages in the gutter downpipe system, or rainfalls which are too light to produce sufficient runoff, or a possible overflow of gutters in the case of an extreme downpour. For this reason we can generally assume that only 90% of the rainwater can be collected.
For calculation we take the following formula:
mean annual rainfall in mm x area in m² x runoff factor = collected rainwater in litres. In our example this means:
450 x 120 x 0.9 = 48 600 litres.
In most cases it would be unrealistic to consider building a cistern of 48.6 m³ capacity for a house with only 120 m² roof area. However, as the situation differs from place to place, we cannot decide here whether a reservoir of this capacity will be realistic and economically efficient.
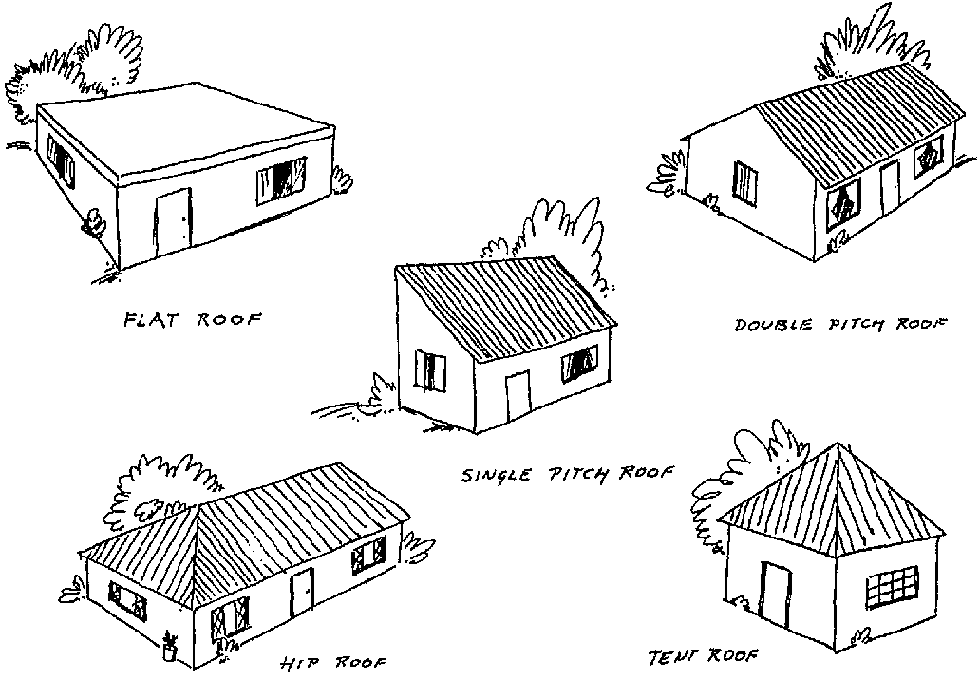
The shape of any given catchment area has a considerable influence on the catchment possibilities. Therefore different types of roofs provide different catchment possibilities. Of the most common roof types shown in Fig. 2.2 the single pitch roof is the most appropriate for rainwater harvesting, since the entire roof area can be drained into a single gutter on the lower side and one or two downpipes can be provided depending on the area. A more difficult roof for rainwater catchment is the tent roof. It requires a gutter on each side and at least two downpipes on opposite corners. If a tent roof is large enough, it could be drained into four tanks located at each corner of the house. The main problem is always the corner. A 90° angle in the gutter should be avoided. It is extremely difficult to adjust gutters in such a way that water really flows easily downwards. It seldom works well when downpours occur, and it is the heavy downpours that should be caught. The hip roof is not very efficient either, since it also needs gutters all around the building. Flat roofs can be used for catchment if they are furnished with an edge, keeping the water on the slab until it has drained through the gutter or downpipe. However, using a flat roof for rainwater harvesting is not very efficient because of the extended runoff-time and the evaporation losses. One way to improve the catchment is to provide the slab with a sloping cement screed. Constructing a waterproof edge on a flat roof is rather difficult because of the temperature expansion.
The most useful roofs are the single and double pitch roofs. The double pitch roof offers many advantages. As the picture of Woodhall Community Centre in Lobatse, Botswana, shows, the gutter of the length of one side can be drained into a reservoir on the other side of the building by fixing the downpipe at the gable wall and sloping it towards the cistern.
Not all materials used for roofing finishes are equally good; but the most commonly used material, metal sheeting (corrugated galvanized iron and aluminium sheets), is very suitable for rainwater catchment; likewise, brick tiles of all variations, and also thatch can be used, but these are less efficient.

 4. How to choose the size of a reservoir
4. How to choose the size of a reservoir
Example I {see Fig 2.3}:
A house with a roof area of 9.00 x 6.50 m is to be furnished with catchment and storage facilities. The mean annual rainfall is 450 mm.
Calculation of rainwater:
9.00 x 6.50 x 450 x 0.9 = 23895 litres
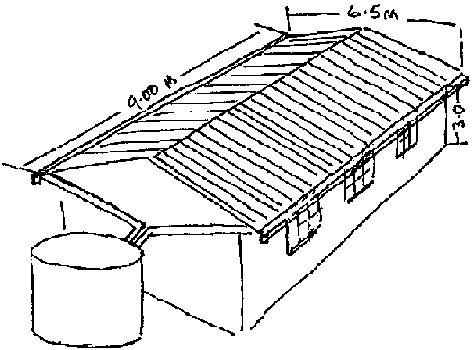
The height from the ground to the gutter outlet is 3.00 m. According to Table 5, a reservoir of 4.0 m diameter on a filling height of 1.80 m has a storage capacity of 23 000 litres. This means that one reservoir built' et one gable side of the house would be sufficient for nearly all the rainwater which can be collected if an average rainfall occurs. Two gutters along the sides of the building should be connected with downpipes fixed to the gable wall and then bridged into the tank.
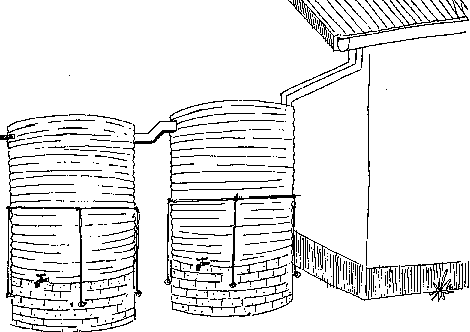
For this storage capacity a ferro-cement tank would be more economically efficient than the reinforced bricktank and serves the same purpose. But if a smaller storage capacity would be sufficient, or if funds are very limited, two corrugated iron tanks, each of 9 000 litres, would be cheaper. These two tanks could be located at each of the gable sides, collecting from each gutter, or next to each other on slightly different levels, draining 'the overflow from the ' tank connected to the pipes into the second tank. Fig. 2.4 shows this as an example with two corrugated iron tanks, but the same method is certainly possible with any other type of reservoir.
Example 2 (see Fig. 2.5): Calculation of catchment area:
Roof A:
20.0 x 10.0 x 450 x 0.9 = 81000 litres
Roof B:
9.0 x 15.0 x 450 x 0.9 = 54 000 litres

Total catchment per annum = 135 675 litres. About 136 m³ of rainwater can be caught within a year from 450 mm rainfall.
The size of the chosen reservoir depends on the lowest inflow (see Fig. 2.5) and also on the ground space available. Block B has a gutter height of 3.00 m, Block A height of 3.30 m. The lowest inflow would come from Block B. Since gutters and downpipes must slope towards the inflow, the height has to be calculated. For the gutters a 0.3% slope is the minimum requirement (equivalent to 3 mm per metre). Block A has a gutter length of 20.0 m (20 x 3 = 60 mm), a downpipe with a minimum slope of 10% (10 mm per metre) to the middle of the gable wall 5.0 m, which means another 50 mm for sloping.
We add the 60-mm slope of the gutters to the 50-mm slope of the downpipe resulting in 110 mm and add 15 mm for the distance from the gable wall to the tank inflow, resulting in 125 mm. For imprecise workmanship, measuring faults etc. we assume a total of 200 mm. These 200 mm have to be deducted from the height of 3.00 m between gutter and ground. This final measurement is 2.80 m and indicates the lowest inflow level and at the same time the filing height of the tank assuming that the bottom of the reservoir is level with the ground. The catchment capacity is about 135 000 litres at the most, with a filing height of 2.80 m. Table 5 shows a filling height of 2.65 m. With this filling height, we can build a reservoir with 133 000 litres with an internal diameter of 8.00m.
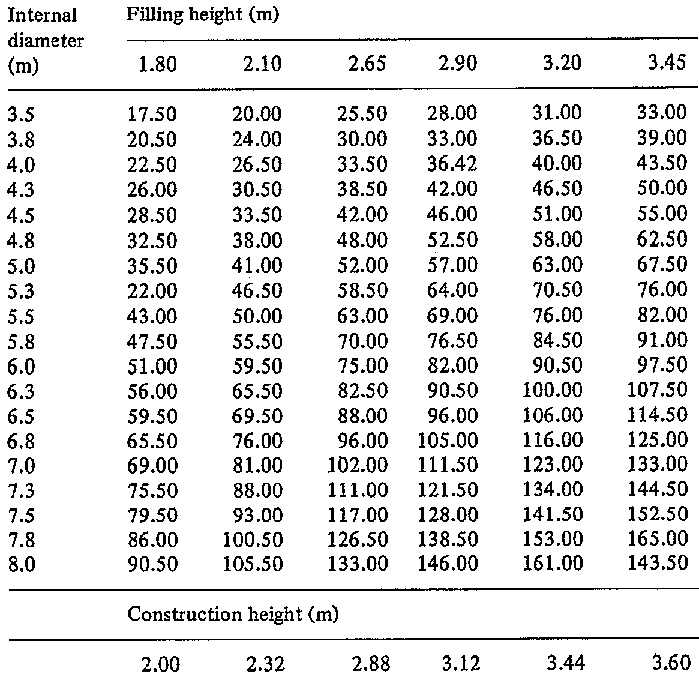
This cistern can only be built as a reinforced bricktank. It will be more economical to build one reservoir of this capacity rather than two reservoirs of about 66 0001, with a filing height of 2.0 m and an internal diameter of 6.5 metres. This example also shows that the correct siting of the building is essential for an economic rainwater reservoir. Taking the theoretical case that the entire rainfall occurs in only 5 days, that would mean that by dividing 135 0001 by 360 days per year, this reservoir would provide 375 litres per day throughout the whole year. Certainly this is theory and in reality the rainfall normally is spread over a period of some months. This also means that some of the collected water will already have been used when the next rain occurs and the reservoir will never be filled up to its maximum capacity, even if the rainfall reaches the annual mean. Or the other way round, since the mean annual rainfall is a statistical measure taken over many years, the chance is greater that an annual rainfall above the average but dispersed over a period of four months will occur and since consumption is constant, even this higher amount of rainwater can be stored.

