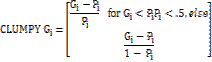Data and Methods
The time series spatial data acquired from Landsat Series Multispectral sensor (57.5 m), thematic mapper (28.5 m), Enhanced thematic mapper sensor and Aster data for the period were downloaded from public domain [36]. Table 1 summarises the data acquired for analysis.
Table 1. Data used for LULC analysis.
Data |
Year |
Purpose |
Landsat Series MSS(57.5 m) |
1977 |
Land use dynamics analysis |
Landsat Series TM(28.5 m) |
1992, 2000 |
|
Landsat Series ETM+(28.5 m) |
2010 |
|
Landsat 8 (28.5 m) |
2014 |
|
ASTER(30 m) |
2011 |
Digital Elevation Model |
Survey of India (SOI) toposheets of 1:50000 and 1:250000 scales |
|
To Generate boundary and Base layer maps. |
Pre-calibrated GPS |
|
Ground control points, attribute data |
3.1. Data analysis
The analysis was a 5 step process as shown in Figure 3.
a). Pre-processing. The remote sensing data (Table 1) obtained were geo-referenced, rectified and cropped pertaining to the study area. Geo-registration of remote sensing data (Landsat data) has been done using ground control points collected from the field using pre calibrated GPS (Global Positioning System) and also from known points (such as road intersections, etc.) collected from geo-referenced topographic maps published by the Survey of India. The Landsat satellite 1977 image have a spatial resolution of 57.5 m × 57.5 m (nominal resolution) were resampled to 28.5 m comparable to the 1992–2014 data which are 28.5 m × 28.5 m (nominal resolution) using nearest- neighbourhood resampling techniques.
b). Land use analysis. Land use categories were classified using supervised classifier based on Gaussian Maximum likelihood (GML) algorithm [37]. Remote sensing data are processed using signatures from training sites to quantify the land-use of Bhopal city broadly into four classes – built-up, vegetation, water bodies and others (detailed in Table 2).
Table 2. Land use classification categories adopted.
Land use class |
Land uses included in the class |
Urban |
Residential area, industrial area, and all paved surfaces and mixed pixels having built up area |
Water bodies |
Tanks, lakes, reservoirs |
Vegetation |
Forest, cropland, nurseries |
Others |
Rocks, quarry pits, open ground at building sites, kaccha roads |
False colour composite of remote sensing data (bands – green, red and NIR), was generated to visualise the heterogeneous patches in the landscape. The signatures were generated as polygons from heterogeneous patches and the attribute information corresponding to these polygons were obtained from the field using pre-calibrated Global Positioning System (GPS) and Google Earth [38]. Among the training data, 60% is used for classification using GML and the balance is used for validation of classified information /accuracy assessment.
c). Zone-wise gradient analysis. The study region consisting of the city boundary and 10 km buffer is divided considering the Central pixel (Central Business district) into 4 zones based on directions as Northeast (NE), Southwest (SW), Northwest (NW), and Southeast (SE). This has been done as most of the definitions of a city or its growth are defined based on directions. The growth of the urban areas was assessed in each zone through the computation of temporal urban density for different period.
d). Gradient Analysis - division of zones into concentric circles. Each zone was divided into concentric circles of incrementing radius of 1 km radius from the centre of the city, and this analysis helped in visualising the process of changes at local levels with the agents responsible for changes.
e). Characterising Sprawl using Landscape Metrics. Landscape metrics provide quantitative description of the composition and configuration of urban landscape.
Table 3. Select metrics for urban growth patterns analyses (metrics prioritised as per Ramachandra et al., 2012a, 2014).
Indicator |
Formula |
Number of patches (Built-up) |
NP = |
Total edge (TE) |
|
Normalised landscape shape Index |
|
Clumpiness Index (Clumpy) |
|
Empirical studies on urbanisation and urban sprawl have demonstrated the usefulness of metrics to understand the spatial patterns of urban sprawl. Four spatial metrics chosen [1] [17] based on complexity, fragmentation, patchiness, and dominance in terms of structure, function, and to characterize urban dynamics were computed zone-wise for each circle using classified land use data at the landscape level with the help of FRAGSTATS [39].
The metrics include the patch area (Largest Patch index), number of urban patches, edge/border (total edge (TE)), and shape (Normalize Landscape Shape Index (NLSI)), epoch/ contagion/ dispersion, Clumpiness were computed for each region for understanding the process of changes at local levels.
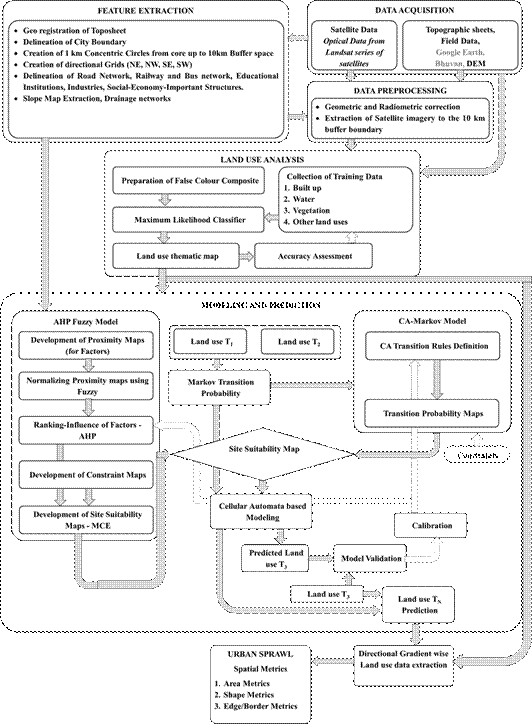
Fig. 3. Procedure adopted for analysis.
3.2. Modelling of urban dynamics using Markov-cellular automata
Markov chain. Markov chain is based on a random phenomenon with the past changes (which affects the future through the present). The “time” can be discrete (i.e. the integers), continuous (i.e. the real numbers), or, more generally, a totally ordered set. The basic assumption in the model is that, the state at some point in the future (t+1) can be determined as a function of the current state (t). Space is assumed as discrete and changes as a stochastic process [40] mainly based on probabilities.
Mathematically formulated as:
X (t+1) = f(X (t)) (1)
where: t – time.
A stochastic process {Xt} satisfies the Markovian property if:
P(Xt+1 = j|X0=k0, X1=k1, …, Xt-1=kt-1, Xt=i) = P(Xt+1=j|Xt=i)
(2)
For all t = 0, 1, 2, … and for every possible state.
A stochastic process {Xt, t = 0, 1, 2, …} is a finite-state Markov chain if it has the following properties:
- a finite number of states;
- stationary transition properties, pij;
- a set of initial probabilities, P(X0=i), for all states i.
Main variables are LULC data, Markov transition (generated using Markov model), a transition suitability image (includes each class suitability images) developed by comparing the suitable sites and constraints for urban class and for other classes the Markov conditional probability images, based on the probability of each class occurrence in each pixel according to past experiences, used as suitability images. A contiguity filter is used for generating a spatially explicit contiguity weighting factor to change the state of cells based on its neighbourhoods.
Cellular Automata (CA). CA are spatially explicit, dynamic, discrete space and time systems [41]. A cellular automaton system consists of a regular grid of cells, each of which can be in one of a finite number of k possible states, updated synchronously in discrete time steps according to a local, identical interaction rule [28]. The state of a cell is determined by the previous states of a surrounding neighbourhood of cells and are [42]. The main components of CA are “cells”, “states”, and “neighbourhood and transition rules”. It is called discrete dynamic system which means the state of each cell at time t+1 is determined by the state of its neighbouring cells at time t, leading to transition rules.
CA induces spatial allocation, location of change into the model and Markov chains predict changes in the properties of land quantitatively, based on historical patterns, which are basic inputs to CA [43]. Global research [44-46] affirms that MC-CA efficiently simulates urban growth patterns.
Validation. These models are typically calibrated using training data (i.e., past land use maps) which are then compared with an actual land use map, and kappa index [47]. The calibrated model can be applied to the prediction of future urban spatial patterns [48].
3.2.1 Agent Based Modelling
Modelling future urban land-use scenarios has been done by integrating developmental factors using an agent-based model (ABM). The model was calibrated by simulating land use for 2014 and compared with the actual land uses and then a 4-year simulation was performed. The goals of this model are to predict future land-use development under existing spatial policies
Characterising influence of each agent using Fuzzy: Fuzzy logic is integrated into modelling methods in order to resolve representation of values in a derived complex environment [49]. Fuzzy rules expressed for each of the variable consist of a set of fuzzy expressions allowing the evaluation of specific attributes considering distances as a measure with simultaneous application of several rules is allowed and with varying membership degrees [50]. Finally distance of influence are measured and provide input to weighing process such as Analytical hierarchal process based on influence a distance with high membership degrees. In this study each agent with different degree of membership and representation function were utilised to derive the influence of distance characteristics which eventually become an input to explain its importance and influence in urban developments.
Weights of influence derived from Analytical Hierarchal Process (AHP): This approach helps in multi criteria decision making (MSDM). The AHP is one of the most commonly MCDM technique incorporated into GIS-based suitability procedures [51][52][53]. Further, these weights are used to generate Markov transition probabilities and in turn these probabilities are used in prediction of urban growth using Cellular Automata.