
 |
| |||
|
|
| 11 of 30 |
| This Document | ||
| SummaryPlus | ||
| Full Text + Links | ||
| PDF (471 K) | ||
|
| ||
| Actions | ||
| Cited By | ||
| Save as Citation Alert | ||
| E-mail Article | ||
| Export Citation | ||
Hydroelectric resource assessment in Uttara Kannada District, Karnataka
State, India
T. V. Ramachandra![]() *,
D. K. Subramanian and N.
*,
D. K. Subramanian and N. ![]() V.
V.![]() Joshi
Joshi
Centre for Ecological Sciences, Indian
Institute of Science, Bangalore 560012, India
Available online 22 April
1999.
The amount of power available at a given site is decided by the volumetric flow of water and the hydraulic head or water pressure. In hydro schemes, the turbines that drive the electricity generators are directly powered either from a reservoir or the `run of the river'. The large schemes may include a water storage reservoir providing daily or seasonal storage to match the production with demand for electricity. These schemes have been producing power in Karnataka for many years, with the first hydroelectric station built in 1942. The majority of them are in Uttara Kannada district. Due to environmental constraints, further construction of storage reservoirs is limited and attention has been focussed towards developing environmental friendly small-scale hydro schemes to cater for the needs of the region. In this paper, the assessment of potential carried out in the streams of Bedthi and Aghnashini river basins in Uttara Kannada district of Western Ghats is discussed. Potentials at five feasible sites are assessed based on stream gauging carried out for a period of 18 months. Computations of discharge on empirical/rational method based on 90 years of precipitation data and the subsequent power and energy values computed are in conformity with the power calculations based on stream gauging. It is estimated that, if all streams are harnessed for energy, electricity generated would be in the order of 720 and 510 million units in Bedthi and Aghnashini basins, respectively. This exercise provides insight to meeting the regional energy requirement through integrated approaches, like harnessing hydro power in a decentralized way during the monsoon season, and meeting lean season requirements through small storage, solar or other thermal options. Net energy analyses incorporating biomass energy lost in submergence show that maximization in net energy at a site is possible, if the hydroelectric generation capacity is adjusted according to the seasonal variations in the river's water discharge.
Author Keywords: catchment area; electric energy; hydro power; million units (m kWh); precipitation; run-of-river plants; small hydro plants; stream flow
Index Terms: Hydroelectric power; Stream flow; Precipitation
(meteorology); Discharge (fluid mechanics); Hydroelectric power plants; Run of
river plant; Hydroelectric resource assessment ![]()
Hydraulic potential is the combination of the possible flows and the distribution of gradients, and the hydraulic resource is that fraction of the hydraulic potential which is still accessible after economic considerations. Hydro power owes its position as a renewable resource to the varying, but more or less continuous flow of a certain amount of water in the stream. Hydro power is a precipitation-dependent resource and is thus subject to the uncertainties which this entails.
Industrialization created new requirements, which demanded increased power generating capacities. The capacities of hydro power plants become very large and now contribute significantly to the State's and National demand. Unfortunately, the cost of exploiting water power is vigilance in ensuring the environment is not irreparably damaged and the life of the river continues to flourish. This demands considerable care and attention in the planning process.
Mini, micro and small hydro plants (A) combine the advantages of large hydro plants on one hand and decentralized power supply on the other. These can divert only potential energy of the water which would have been dissipated to no benefit in the natural flow. The disadvantages associated with large hydro power plants, high transmission costs, environmental costs of submergence of prime lands (forests, crop lands, etc.), displacement of families etc., are not present in the case of small plants. Moreover, the harnessing of local resources, like hydro energy, being of a decentralized nature, lends itself to decentralized utilization, local implementation and management, rural development mainly based on self reliance and the use of natural, local resources. The domain where these plants can have potential impact on development is domestic lighting and stationary motive power for diverse productive uses like water pumping, wood and metal work, grain mills, agro processing industries, etc.
Uttara Kannada District located in the mid-western part of Karnataka state (Fig. 1) is selected for this study. It lies 74° 9' to 75° 10' east longitude and 13° 55' to 15° 31' north latitude and extends over an area of 10291 sq km, which is 5.37% of the total area of the state, with a population above 12 lakhs. It is a region of gentle undulating hills, rising steeply from a narrow coastal strip bordering the Arabian sea to a plateau at an altitude of 500 m, with occasional hills rising above 600 to 860 m. According to the recent landsat imageries, of the 10291 sq km geographical area, 67.04% is under forest, 1.94% under paddy and millet cultivation, 1.26% under coconut and areca garden, 1.94% under rocky outcrops and the balance 27.82% is under habitation and reservoirs. There are four major rivers––Kalinadi, Bedthi, Aghnashini and Sharavathi. Besides these, many minor streams flow in the district.
Fig. 1. Uttara Kannada District, Karnataka.
This district with 11 taluks can be broadly categorized into three distinct regions––coast lands (Karwar, Ankola, Kumta, Honnavar and Bhatkal taluks), mostly forested Sahyadrian interior (Supa, Yellapur, Sirsi and Siddapur taluks) and the eastern margin where the table land begins (Haliyal, Yellapur and Mundgod taluks). Climatic conditions ranged from arid to humid due to physiographic conditions ranging from plains, mountains to coast. This large variety of natural conditions provides the basis for generalization of the theoretical probability distributions for annual precipitation. Among the four rivers, the hydro potential of Kali and Sharavati has been tapped already for power generation. The completed large scale projects have caused serious environmental damage in the form of submergence of productive natural virgin forests, horticulture and agricultural lands, etc. In view of these, we assess the potential of the Bedthi and Aghnashini rivers and explore ecologically sound means of harnessing the hydro energy.
The choice of site is based on a close interaction between the various conditions like the pattern of the stream, integrity of the site works, environmental integration, etc. It is necessary to establish the inventory of energy demand in various sectors and assessment of various other sources like solar, biomass, wind, etc. Various factors considered while estimating hydro potential are: (1) the head; (2) hydrological pattern: defined from measurements or from inter-relationships between effective rain and discharge; (3) usage of water, upstream of the intake to determine the flow which is available, and downstream to determine the effects of diverting the water from present and future uses; (4) distance from the intake to the power station and from the power station to the consumer site; and (5) size of the scheme involved and evaluation of their stability depending on various lithological, morphological and topographical conditions.
The objectives of this endeavour are to assess the potential of:
1. The streams based on 18 months field survey carried out in the basin of the Bedthi river;
2. The streams in the Bedthi and Aghnashini river basins based on precipitation and topographical information, and to explore an environmentally sound storage option.
The hydrology of the river and streams under consideration were studied by:
1. Reconnaissance study: an exploratory survey was carried out in all streams which satisfy the above listed criteria and with water head greater than 3 m;
2. Feasibility study: this involved measurement of the catchment area and stream discharge for a substantial period of time.
Catchment boundaries are located using the contour lines on a topographical map. Boundaries are drawn by following the ridge tops which appear on topo maps as downhill pointing V-shaped crenulations. The boundary should be perpendicular to the contour lines it intersects. The tops of mountains are often marked as dots on a map, and the location of roads which follow ridges are other clues. The catchment area thus marked/traced is measured directly from the marked maps using a planimeter.
Both direct and indirect methods were carried out. The indirect method is tried in order to assess the potential of ungauged streams.
Stream discharge is the rate at which a volume of water passes through a cross-section per unit of time. It is usually expressed in units of cubic meters per second (m3/s). The velocity–area method using a current meter is used for estimating discharge. The cup type current meter is used in a section of a stream, in which water flows smoothly and the velocity is reasonably uniform in the cross-section. This measurement is carried out for three consecutive days every month for 18 months in order to take into account day-to-day fluctuations and seasonal variations. Five readings are recorded each time and the mean value is computed.
Runoff is the balance of rain water, which flows or runs over the natural ground surface after losses by evaporation, interception and infiltration. The yield of a catchment area is the net quantity of water available for storage, after all losses, for the purpose of water resource utilization and planning. The runoff from rainfall was estimated by (1) the empirical formula and (2) the rational method.
1. Empirical formula: the relationship between runoff and precipitation is determined by regression analyses based on our field data.
2. Rational method: a rational approach is used to obtain the yield of a catchment area by assuming a suitable runoff coefficient.
| Yield=C*A*P |
This involved (i) analyses of 90 years' precipitation data collected from the India Meteorological Department, (ii) computations of discharge by the empirical/rational method based on precipitation history of the last 90 years and comparison with the values obtained by actual stream gauging, and (iii) computation of discharge and power in ungauged streams by the empirical/rational method in the Bedthi and Aghnashini basins.
Computation of power and total energy available in all streams.
The response of watershed to precipitation is the most significant relationship in hydrology. The complexity of the rainfall–runoff relationship is increased by the areal variations of geological formations, soil conditions and vegetation, and by the areal and time variations of meteorological conditions [2]. Vegetation influences the rainfall–runoff relationship not only through interception and surface detention, but also by its effect on the impact energy of rainfall, which may initiate turbulence in overland flow and increase erosion.
The extent to which a stream/river is developed for energy depends on their flow, design of plant, etc. Precipitation and river flow are governed by chance phenomena, that is, there are so many causes at work that the influence of each cannot be readily identified. Therefore, statistical and probability methods are applied to describe this hydrological phenomena [3]. An attempt is made in this section to (1) find theoretical probability functions of best fit relationships to distributions of annual precipitation and (2) find whether there is any relationship in year-to-year precipitation, and to see whether this data reveals any significant trend.
Most rainfall records are obtained by periodic observation of gauges. The usual interval is 24 h. In this district, the India Meteorological Department has three observatories in coastal belts at Karwar, Honnavar and Shirali, where various parameters like temperature, humidity, rainfall, solar radiation and cloud cover are recorded at regular intervals through automatic weather stations. In 27 rain gauge stations distributed all over the district rainfall is recorded manually, usually through Tahsildar's office. All precipitation records collected from various agencies are used with the realization that the records obtained (at different elevations) are indicative of average precipitations.
The inter annual variability of the yearly and monsoon rainfall has considerable impact on activities like agriculture, water management and energy generation. In view of this, monthwise rainfall data collected all over the district and subsequent annual rainfall variability computed have been looked at in greater detail. Ankola, Bhatkal, Kumta, Karwar, Sirsi, Siddapur and Yellapur taluks' rainfall variability were studied for 90 years, beginning from 1901. However, the data were studied in Haliyal taluk for 22 years, Supa taluk for 27 years and Honnavar taluk for 62 years. The annual average rainfall and standard deviation computed for each taluk based on these data are listed in Table 1. This shows that Bhatkal receives the highest rainfall, of the order 3942 (avg)±377 (SD) mm and Haliyal, least rainfall with 1174 (avg)±166 (SD) mm. The coefficient of variation computed to see the relative variability of precipitation data is listed in Table 2. The coefficient of variation ranges from 0.085 (Karwar) to 0.1105 (Honnavar) in the coastal region, 0.0810 (Yellapur) to 0.1217 (Siddapur) in the Sahyadrian interior, and 0.1415 (Haliyal) to 0.2083 (Mundgod) in the plains.
Table 1. Annual rainfall––Talukwise
(<1K)
Table 2. Talukwise computation of coefficient of variation (COV)
(<1K)
As indicated in Fig. 2, the coastal taluks receive the highest mean annual rainfall of 3132 to 3942 mm. The hilly taluks follow the coastal taluks with 2470 to 2997 mm. The taluks in the plains get the least rainfall. It is seen that the ranges of annual precipitation are very distinct, indicating the large variety of the climatic and physiographic area of the district. The south west monsoon constitutes 88 to 90% of total precipitation in these taluks. Various statistical tests are carried out for annual rainfall data for each taluk to find out whether the rainfall regime in any taluk follows a particular trend, whether there is any relationship among variables and to see whether the rainfall during any particular year depends on previous year/s. The statistical runs test (runs above mean and below mean, runs up and runs down) conducted for annual rainfall data for each taluk and the district suggests that the variables are independent of each other.
Fig. 2. Mean annual rainfall (Talukwise) Uttara Kannada District.
According to properties of observed data, the distribution functions of best fit to observed frequency of annual precipitation should be a bell-shaped but skewed curve. Screening of the applicable functions with respect to the criteria required, their convenience in usage in mass computation, and the experience already obtained in applying them in this kind of analysis, as listed in the literature [4, 5], lead to the selection of (a) normal density function, (b) log normal and (c) gamma.
To test the theoretical probability distribution functions for goodness of fit to observed data, the data is classified into mutually exclusive and exhaustive categories of class intervals. The chi-square test is used as a measure of goodness of fit of the theoretical probability distributions. If the probability of a hypothesized function is less than the assigned level of significance, then the function would be acceptable as a good approximation to the distribution of a considered sample. The normal and log-normal distributions are fitted to the distribution of annual precipitation data of taluks in Uttara Kannada district. It is found that the departure between normal and observed distribution would give the probability of chi-square less than 0.95 for Siddapur, Yellapur, Karwar, Mundgod, Haliyal and Supa taluks. While for Ankola, Kumta, Sirsi, Bhatkal and Honnavar taluks, annual precipitation data follows log-normal distribution, as the departure between observed and log-normal distribution has the probability of chi-square 0.32, 0.55, 0.82, 0.44 and 0.79 (all are less than 0.95, accepted at the 95% level of significance). The smaller the value of probability, the smaller is the departure between theoretical and observed distributions, and the better the theoretical function fits an observed distribution.
These analyses illustrate that altitude and distance from the sea cannot explain the differences between the distributions of annual precipitation of taluks. For example, two neighboring taluks in the coastal belt, Ankola and Karwar (or in the interior, Siddapur and Sirsi), give two different distributions. There may be certain other factors, such as latitude, temperature, evaporation, prevailing wind direction of moist air masses, governing the difference in distribution. However, analyses show that regional characteristics especially do not favour the use of one of the probability functions in fitting the observed distributions of annual precipitation.
Distributions of annual river and stream flows are affected by physiographic factors of a watershed area apart from its precipitation. The literature regarding watershed response can be classified into two general groups. The majority of the research has dealt with obtaining the time distributions of direct surface runoff at a point, given the volume and distribution of the effective rainfall. The remaining part deals with the total rainfall–runoff relationship, including estimation of the volume of effective rainfall, considering loss functions experienced by storm rainfall. Studies regarding the conversion of effective rainfall to hydrographs of stream flow at the catchment outlet stem primarily from unit hydrograph theory. The theory has been modified, applied, verified, and used for analysis and synthesis. The concept of the instantaneous unit hydrograph along with various storage and routing ideas has led to numerous theoretical response models. On the other hand, few rainfall–runoff models have been investigated with emphasis on the conversion of rainfall to effective runoff.
Stream flow and ecology are both affected by catchment conditions. Changes in stream discharge and sediment loading, caused by the modification of the catchment area are reflected in variations in the rate of sediment transport, channel shape and stream pattern. Responses to a change may be immediate, delayed or dependent upon a critical factor reaching a threshold level. It is necessary to know the response of catchment/watershed to rainfall in order to design structures, such as overflow spillways on dams, flood-protection works, highway culverts and bridges [6]. The rate at which runoff moves towards the stream depends on the drainage efficiency of the hill slopes. Drainage efficiency is influenced by the slope and length of upland surface, its micro topography, the permeability and moisture content of the soil, subsurface geology and vegetation cover. The hydro potential of each stream is assessed so as to have micro, mini or small hydro power plants.
The catchment area for streams are obtained from the Survey of India toposheets. Stream gauging is done with both direct and indirect methods.
Catchment area measured from the marked toposheets using planimeter for the streams in Bedthi and Aghnashini river basins are listed in Table 3 and Table 4, respectively. Along the Bedthi river course drops at various points have been identified: Kalghatgi (80 m), Kaulgi Halla (64 m), major drop at Magod (of about 340 m), and the lowest drop 8.5 m is in Ankola taluk, about 129 km from Kalghatgi. Numerous streams join the river along its course from Kalghatgi. Major streams with good drops (head) are Shivganga (119 m), Handinadi (230.50–318.50 m) and Matti gatta (270 m). The Aghnashini river has major drops at Unchalli (360 m) and the major streams are Benne (400 m drop), Bhimavara (290 m), Mudanalli (270 m), etc.
Table 3. Catchment area, stream slope, catchment slope computed for various streams of Bedti river
(<1K)
Table 4. Catchment area, stream slope, catchment slope computed for various streams of Aghnashini river
(1K)
The average channel slope (Sc) is one of the factors controlling water velocity, while the slope of the catchment (Sb) influences surface runoff rates. These two parameters give an idea about the nature of a stream. Hence Sc and Sb are computed and listed in Table 3 and Table 4. Magod has a slope of 61.34°. The Shivganga and Mattigatta streams of the Bedthi catchment have slopes 43.83° and 40.03°, while Muregar and Boosangeri have slopes of 6.27° and 2.29°. The Muregar jog has a catchment of 25.97 sq km, while Boosangeri has 11.29 sq km. Stream gauging at regular intervals is carried out in Muregar, Boosangeri, Vanalli and Shivganga.
The shape of the Boosangeri catchment is short and wide (fan shaped), while Muregar, Mattigatta and Shivganga catchments are elongated.
Stream gauging is carried out using a current meter every month. Stream discharge ranges from 1.12 (August) to 0.015 cum/s (in February) for Boosangeri. In the case of Muregar, it ranges from 1.395 to 0.026 cum/s. This indicates that streams of this kind are seasonal. Power generated during June to September is sufficient to meet the energy needs of the nearby villages. Power computed for these streams is shown in Fig. 3.
Fig. 3. Estimated power in Muregar and Boosangeri (based on field experiments).
Stream flow measurement (indirect method)––empirical formula: the runoff (R) and precipitation (P in cm) relationship determined by regression analyses based on our field data R=0.85*P+30.5, with r=0.89 and the percentage error is 1.2.
In order to estimate the hydro power potential of ungauged streams, either the rational or empirical relationship of runoff and precipitation is used. In the rational method, monthly yield is derived by assuming a suitable runoff coefficient (which depends on catchment type). For each site, Yield (Y=C*A*P) is computed with the knowledge of catchment area (A), catchment coefficient (C) and precipitation (P). An attempt has been made to compute the monthly yield from catchments by this method, and subsequently the power that could be harvested from the streams. Estimated monthly power by the indirect method is shown pictorially in Fig. 4. This corresponds with the power computed by the direct method (of the gauged streams Boosangeri and Muregar). Hence, we use the rational method to compute hydro power of ungauged streams. This study explores the possibility of harnessing hydro potential in an ecologically sound way (by having run-of-river plants with no storage options) to suit the requirements of the region. The Sirsi, Siddapur and Yellapur taluks in hilly terrain amidst evergreen forests with a large number of streams are ideally suitable for micro, mini or small hydro power plants. Monthly stream gauging at Muregar and Boosangeri has revealed that mini hydro power plants could be set up at these sites. The stream at Muregar is perennial, with a flow of about 0.26 m3/s during summer, and power of the order of 10–20 kW could be generated, while during the monsoon power of 300–400 kW could be harnessed.
Fig. 4. Estimated power in Muregar and Boosangeri Jog (rational method).
Computations of discharge by the empirical or rational method, considering precipitation history of the last 100 years, and the subsequent power calculated is in conformity with the power calculations done based on stream gauging. Based on this field experience of gauged sites, an attempt has been made to compute water inflow (using the indirect method), hydraulic power available, and energy that could be harnessed monthly for all ungauged streams in the Bedthi and Aghnashini river catchments. The energy potentials of all streams in these catchments are listed in Table 5 and Table 6, respectively. It is estimated that we can generate about 720 and 510 million kWh from various streams in the Bedthi and Aghnashini catchments.
Table 5. Estimated energy ('000 units) in ungauged streams of Bedthi catchment area
(<1K)
Table 6. Estimated energy ('000 units) in ungauged streams of Aghnashini catchment area
(<1K)
The potential assessment shows that most of the streams are seasonal and cater for the needs of local people in a decentralized way during the monsoon. This ensures a continuous power supply during the heavy monsoon, which otherwise gets disrupted due to dislocation of electric poles due to heavy winds, and the falling of trees/branches on transmission lines, etc. A detailed household survey of villages in hilly areas shows that, during the monsoon, people have to spend at least 60 to 65% of the season without electricity from centralized supply due to environmental problems. This demands for alternatives to meet the region's requirement during the lean season. This exercise provides insight into the regional energy requirement through integrated approaches like harnessing hydro power in a decentralized way during seasons and meeting the lean season requirement through small storage option, solar or other thermal options. In view of this, an ecologically sound alternative is proposed, which would generate maximum electricity during the monsoon and sufficient electricity during the lean season by storing enough water to meet the region's requirements.
Nature does not meet the demand for water at all times and in all places. Due to environmental impacts associated with large reservoirs, it has become necessary to estimate their proper sizes to meet the target demand of a region. The design of storage systems for power generation in a hilly terrain is constrained mainly by ecological factors these days. The negative aspects of hydroelectric projects necessitate the minimizing of the submergence area and are subject to reasonable costs, minimum or no wastage of water and seasonal constraints (the region receives maximum rainfall during the south-west monsoon).
1. Assumptions: detailed geological and topographical investigations carried out to determine the best site for the dam, pressure shaft alignment, power house location, etc. by the Department of Mines and Geology and Karnataka Power Corporation Limited [7], can be used for implementing this design.
2. Parameters: input data consists of site specific (discharge, water yield, generation head, evaporation rate, seepage rate etc.), technical (efficiency of turbine and generator, and dependability norm for storage capacity, load factor, etc.) and economic data (civil construction costs for various types and heights of dam, cost of electrical machineries of various capacities, environmental costs, rehabilitation costs, etc.).
3. Decision variables: these are to determine the optimum storage capacity, installed generation capacity and seasonal power drafts, to maximize net energy availability in the region (objective function) subject to seasonal hydrological constraints, and minimize costs and submergence area.
The broad outline of an optimization model for exploiting a river for hydro power and irrigation, incorporating energy costs and net increase in yield due to irrigation, with constraints on arable area and crop water requirements and seasonal variations in precipitation, was formulated earlier by Subramanian [8]. On the same lines, with detailed engineering design and quantification of data, the parametric optimization approach is used, to find out the alternatives for the Magod site, to get maximum energy subject to the ecological constraints.
The parametric model is solved for various scenarios for optimal utilization of energy in the water and thermal energy in the region. The objective is to maximize the net energy available in the region, which is given by
| Enet=Eh-Ebio | (1) |
This model includes an equation which computes monthly hydro power production as a function of (a) the volume of water discharged, (b) the gross head of this water, and (c) the efficiency of the couple turbine generator. Hydro power is given by
| P=9.81* Q*H | (2) |
The corresponding electricity produced Eh=P*t*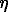 , where
E is the electricity produced (in kilowatt hours), P is the
hydraulic power (in kilowatts), t is the operating time (in hours) and
, where
E is the electricity produced (in kilowatt hours), P is the
hydraulic power (in kilowatts), t is the operating time (in hours) and
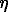 the
turbine-generator assembly efficiency (between 0.7 and 0.85). Because of the
estimates of the couple turbine-generator and gross height, this is only an
approximate characterization of the energy harnessed for the purpose of
illustration.
the
turbine-generator assembly efficiency (between 0.7 and 0.85). Because of the
estimates of the couple turbine-generator and gross height, this is only an
approximate characterization of the energy harnessed for the purpose of
illustration.
The monthly hydroelectricity generated in million units (million kWh) is given by
Eht=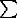 9.81*Dt*H* 9.81*Dt*H*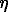 |
(3) |
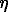 is the
efficiency of the turbine-generator combination and Dt is the
power draft from the reservoir during a month (million cubic meters,
Mm3). This can be written as
is the
efficiency of the turbine-generator combination and Dt is the
power draft from the reservoir during a month (million cubic meters,
Mm3). This can be written as
Eht=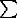 k1*Dt,
where k1=9.81*H* k1*Dt,
where k1=9.81*H*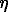 |
Eht=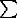 k1*Dtm+ k1*Dtm+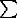 k1*Dtd k1*Dtd |
(4) |
Ebio=Asub*Gr*(CV)*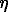 c c |
(5) |
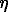 c is the energy conversion
efficiency.
c is the energy conversion
efficiency.
The area submerged is further classified as forest, agricultural lands, gardens, etc. The thermal content of biomass is computed in terms of their primary energy contents. For example, a ton of dry fuelwood with a calorific value of 4400 kcal/kg has a thermal content of 5112 kWh, which is considered equivalent to the same amount of electrical energy. This model is subject to the following constraints:
These operate on a monthly basis and consist mainly of the following continuity equation [9].
| Vt+1=Vt+It-St-Et-Dt | (6) |
1. Functional relationship between volume, surface area and water level;
2. Relationship between seepage and volume;
3. Relationship between evaporation and volume;
4. Sequence of monthly inflows into the reservoir;
5. Policy for determining the discharges from the reservoir; and
6. Volume of the reservoir when the simulation begins.
A certain amount of `dead' storage capacity was added to account for sedimentation.
The storage capacity (V) of any reservoir is the function of both targeted draft (D) and reliability (R), given by
| V=f(D,R) | (7) |
It is seen that the required reliability of the targeted draft has a direct relation to effective storage capacity, which has to be provided. For a given draft, particularly the one approaching a mean flow, the required storage is extremely sensitive to reliability. Likewise for a given level of reliability, an increase in the targeted draft would result in large storage. Thus, for a given draft, storage would increase substantially with increased reliability levels. For hydro planning, in the case of generation schemes, a dependability criterion of 90% is normally adopted. Failure for a month in a decade would mean a reliability of 99.2% on a monthly, but 90% dependability on a yearly basis. This is because, failure in any one month is considered to be failure for the whole year.
| Ptm=Ptd, | (8) |
That is, the hydroelectric generation capacity during monsoon months (Ptm) is same as that during the non-monsoon period (Ptd).
If seasonal variation is allowed, Ptm 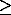 Ptd PtdIf variation of "r" is allowed Ptm 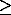 r*Ptd r*Ptd |
(9) |
| Ptm=k1*Dtm/LFtm and Ptd=k1*Dtd/LFtd | (10) |
| Dtm/LFtm=Dtd/LFtd | (11) |
Dtm/LFtm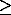 r*Dtd/LFtd r*Dtd/LFtd |
(12) |
| LFtm=LFtd=LF | (13) |
| Dtm=Dtd | (14) |
Dtm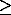 r*Dtd r*Dtd |
(15) |
Active storage capacity Ka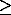 Vt for t=1,2,...12 Vt for t=1,2,...12 |
(16) |
The feasible operating policy, considering seasonal variation in water inflow, would be:
{S1*Ptm+S2*Ptd}*30*24*LF* (amount of water/million units)=Total qty. of water available at site |
| 4*Dtm+8*Dtd=Vt+1 |
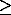 r*Dtd where the value
of `r' ranges from 1, 2...
r*Dtd where the value
of `r' ranges from 1, 2... , and
Vt+1=Vt+It-St-Et-Dt.
, and
Vt+1=Vt+It-St-Et-Dt.
With a change in the dam height, the submergence area and storage volume changes. The submergence area and volume computation is discussed later in case studies. The regulation through storage could be shown as follows:
| Dt=Vt+It-St-Et | (17) |
| Dt+d=Vt+It-St-Et | (18) |
Dt 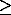 0, for all t=1,2...12 0, for all t=1,2...12and Vt 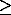 0, for all
t=1,2...12 0, for all
t=1,2...12Therefore, Ka 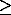 0 0 |
(19) |
This design is implemented for the hydroelectric scheme at Magod.
The hydrology of the Bedthi river was analysed daily and weekly using 5 years' daily precipitation data. The average annual yield at Magod is 1125 Mm3 by the rational method, compared with 1105 Mm3 by the empirical method. Ninety per cent dependable water yield is estimated as 995 Mm3. Water yield computed at Magod by the empirical method with 90 years' precipitation data shows that water quantity varies from 0.25 (avg)±1.25 (SD) during January to 364 (avg)±136 (SD) during July.
These losses are estimated as 99 Mm3 per annum for 100 sq km of the region. About 48% of the basin area is plain with partial vegetation cover receiving moderate rainfall. The remaining area is hilly with evergreen vegetation. The silt rate per annum (S) is given by S=C(A)3/4 where C=4.25 assumed for the basin with plain and forested tracts. For Magod, the silt rate is found to be 0.83 Mm3 per year. At this siltation rate, the life of the reservoir at FRL 450–455 m is about 50 years.
The river Bedthi, flowing in a deep and well defined gorge, drains a total area of 4060 sq km. The site proposed is about 0.91 km upstream of the Magod falls, at longitude 74°45'28''E and latitude 14°51'41''N. This site commands a basin of 2084 sq km and has an exposed rocky bed at the flanks on either side. The river bed level here is 373 m and is 36 m wide. At 450, 460 and 480 m contour elevations, the length of the dam would be 392, 436 and 579 m, respectively.
A dam at this site submerges areas having biomass like firewood, twigs etc. and bio residues of agricultural and horticultural lands, which is used for domestic, commercial and other purposes. This energy is significant. When the water head is very high and the reservoir profile a deep valley with steep walls at its sides can hydroelectric energy be very competitive compared to bio energy. When the water head is not much and the terrain has a slope less than 25°, then the smaller depths of a reservoir with less submergence area make firewood an attractive option.
In order to find the contours of submergence areas corresponding to certain dam heights, Survey of India's 1:50000 scale toposheets are used. The area is computed using a planimeter. The volume of water stored for a particular dam height computed by assuming the volume between two consecutive contours to be trapezoidal is
| V12=(a1+a2)*0.5*h12 | (20) |
.gif) |
(21) |
The submergence area and corresponding volume computed for different dam heights at Magod are depicted in Fig. 5. This shows that, when the dam height is 67 m, the submergence area is 5.7 sq km and the volume is 106.35 Mm3. Beyond 87 m, there is a steep increase in submergence area, as is evident from a submergence area of 95.02 sq km for a dam height of 107 m. The relationship between the submergence area and the height of the dam is found to be either powerlaw or exponential (Asub=0.38*e(0.048*Hdam)) with r=0.99, and percentage error 0.45. Similarly, the probable relationship between the volume of water and the height of the dam is exponential (Vdam=5.03*e(0.054*Hdam)) with r=0.99 and percentage error 0.22 (Fig. 6).
Fig. 5. Dam height and corresponding submergence area.
(7K)
Fig. 6. Dam height and corresponding storage capacity.
We have computed the hydro power equivalent at each site before maximizing the net energy function. Energy from water is computed based on parametric optimization techniques, listed in Table 7. If variation is allowed between Ptm and Ptd, it reduces the storage capacity requirements. By allowing the Ptm to Ptd ratio to be 3, we notice that the submergence area saved is about 69.97%. This results in the reduction of the civil costs of the project. Regression analysis of these variables gives a hyperbolic relationship, given by En=733.86+[(1566.28)/Area]-[(6024.64)/(area)(area)], with r=0.99 and percentage error of 1.04. We harness more hydroelectric energy by drawing the water during the monsoon on a run of river basis and store sufficient quantity to meet the non-monsoon requirements. This saved area would also help in meeting the bio resource requirements of the region. We notice that by allowing variation in the Ptm and Ptd ratio, there is an increase in the electric energy generated. This is because, for smaller heights of the dam, the submergence area is less and therefore evaporation and seepage losses are also less.
Table 7. Power (in mega watts) and energy (in million kWh)
(50K)
The land use pattern in the area to be submerged for various heights of dam shows that the area under natural forest is the major constituent of the submerged land, consisting of evergreen, semi-evergreen and deciduous forests where the primary production of biomass is estimated to range between 6.5, 13.5, 20 and 27.5 t/ha/year [10]. Areca and coconut residues from gardens are in the range of 3–4.5 t/ha/year.
The reduction in submergence area implies a reduction in the loss of thermal energy. The net energy is computed taking the thermal value of bioresidues available in the region and indicates that with a decrease in dam height, the net energy available increases. As indicated in Table 8 at Magod, the net energy increases from 417 (for a dam of 107 m and biomass productivity of 6.5 t/ha/year) to 803 million units (for a dam of 67 m). The efficiency of a hydro power station is the combined efficiency of turbine, generators etc. It is estimated that this efficiency is around 70%. For this scenario, the net energy function becomes
Enet=0.7*Eh-Ebio(lost) Enet=Eh'-Ebio |
(22) |
Table 8. Hydro, thermal energy and net energy available from submerged area (million kWh)
(48K)
To account for only the final amount of electricity, the thermal energy content of source is discounted by the conversion efficiency of a thermal power plant (as 35%). With this
| Enet=Eh'-0.35*Ebio (where Eh' is 0.7*Eh) | (23) |
The result of this computation, given in Table 8, shows that a variation in the net energy available ranges from 407 to 569 million units at Magod.
The domestic fuelwood consumption survey of this region reveals that 82 to 90% of the households still depend on fuelwood and agro residues to meet the domestic cooking and water heating requirements. The annual fuelwood energy requirements are estimated to be 312 million units. System efficiency considerations, peak power considerations and socioeconomic considerations all rule out the possibility of electricity entirely substituting fuelwood as a source of domestic energy. Therefore only a fraction of the wood energy is converted into electrical energy, that is equal to the fraction of the purely non-thermal consumption of electric energy in a total wood and electric energy consumption. A dam height of 107 m at Magod submerges about 95.03 sq km, of which 88.53 sq km is under evergreen and semi-evergreen forests, rich in biodiversity. This necessitates eco-friendly options, to reduce the submergence of prime forests.
The model and subsequent quantitative analyses demonstrates that much of the land could be saved from submergence if the hydroelectric power generation capacity is adjusted according to seasonal variations in the river's runoff. The viability of a mixed hydro and biomass generation system is shown in energy terms, which leads to a significant reduction in the total area used for power generation. Apart from this, there is scope to generate hydroelectric energy from streams in a decentralized way.
Forests play a role not only in the social and economic wellbeing of the society but also in maintaining the ecological balance. With the submersion of forests, benefits such as (a) fuelwood, (b) timber, (c) grass and other biomass material, (d) forest products such as cane, bamboo, gums, resins, drugs, spices, etc., (e) biodiversity, (f) recreation and (g) environmental benefits, such as soil conservation, recycling of water and the control of humidity, etc., are lost. Direct costs of the submerged area are assessed by considering standing biomass in the area, which is based on species diversity studies carried out in sample plots at Sonda, Kallabe, etc. In this computation, the price of forest land is taken as Rs 111200 per hectare.
The costs involved in the submersion of agriculture lands, areca nut gardens and coconut plantations were based on the market value of the land in this region. The value of areca nut garden is Rs 890000 per hectare, while for paddy, it is Rs 99000 per hectare and coconut plantation is about Rs 218000 per hectare. The details of villages submerged and the number of households affected are obtained from government agencies like the Village Accountant's office. The displacement and rehabilitation costs were based on the data from earlier hydroelectric projects.
The capital cost depends on (a) civil construction costs (size and type of dam) and (b) cost of generating unit, which depends on the capacity. The capacity is calculated using a normal load factor of 0.5. The schedule of rates approved by the government recently has been used in computing civil and electrical costs. Annual capital recovery factor (annuity factor) is calculated for the total cost (civil plus electrical plus environmental plus rehabilitation) at 12% interest for 50 years of satisfactory functioning of the power station.
Annual O and M charges are taken as 1% of the total cost of the project. The depreciation works out to be 1.80%, taking into account the life of dam as 70 years, surge shafts, penstock, power house equipment, power house building and substation equipment as 50 years, and roads, etc. as 35 years. Hence, annual cost
| C=Annuity factor*Total cost+O and M charges+Depreciation cost |
With this annual cost and energy information, we have computed cost per unit of energy (see Table 9). Fig. 7 lists cost per unit (cost per kWh). It shows 40.5% reduction in cost (Rs 1.53 per unit to Rs. 0.92 per unit) for a dam height reduction of 32.75%. If we consider electricity from water resources only, then cost reduction is from Rs 1.53 per unit to Rs 1.09 per unit.
Table 9. Cost per unit (kWh) of electricity (considering biomass productivity as 6.5 t/ha/year)
(7K)
(9K)
Fig. 7. Cost (Rs per kWh) of energy for various designs.
The potential assessment of streams in the Bedthi and Aghnashini river catchment shows that most of the streams are seasonal and cater for the needs of local people in a decentralized way during the season. This ensures a continuous power supply during the heavy monsoon, which otherwise gets disrupted due to various problems. This study explores the possibility of harnessing hydro potential in an ecologically sound way to suit the requirements of the region.
Energy that could be harnessed monthly is computed for all ungauged streams in the Bedthi and Aghnashini river catchments based on the empirical or rational method considering the precipitation history of the last 100 years. The hydro energy potentials of streams in the Bedthi and Aghnashini river catchments are estimated to be about 720 and 510 million kWh, respectively.
The net energy analysis explains the upper limit on the height of a dam and, therefore, the area of the reservoir for the project to yield a positive net energy. Also, it is noticed that savings in land submergence could be achieved by adjusting hydroelectric generation capacity according to seasonal variation in the river runoff. The parametric optimization technique is used to compute energy from a hydro source at Magod. By allowing a seasonal generation ratio of 3, the submergence area saved is about 69.97%, and we notice the subsequent increase in electric energy generated. This is mainly due to less evaporation and seepage loss due to a reduced submergence area for smaller dam heights.
Net energy analyses carried out by incorporating the bioenergy lost in
submergence at Magod show a gain of 63.9% for a reduction of 37.3% in dam
height. Apart from the distinct reduction in submergence area, the overall
reliability of a hydro and thermal combined system is much higher than that of
pure hydro systems (which are very sensitive to fluctuations in rainfall). The
fuelwood requirement in the region is about 312 million units (million kWh) for
domestic purposes. The net energy computed for various dam heights indicates
that dams of 67 m height store enough water to meet the region's lean season
electricity requirements, and the area saved has a bio resource potential of 319
million units, which can cater for the thermal energy demand of 312 million
units. The cost per unit for various designs of the dam shows a 40.5% reduction
in cost (Rs 1.53 per unit to Rs 0.92 per unit) for a dam height reduction of
32.75%. ![]()
This research was supported by grants from the Ministry of Environment and
Forests, the Government of India and Indian Institute of Science. We thank Mr
Sampath and Mr Dinesh, Information Analysts, Karnataka State Council for Science
and Technology, for taking part in an exploratory survey to identify feasible
sites and useful tips in field survey and site identification. We thank our
colleagues Mr Deepak Shetti, Mr Rosario Furtado, Mr Kumar and Mr Raghavendra Rao
for their assistance in the collection of stream flow data at regular intervals.
![]()
1. Raghunath HM. Hydrology: principles, analysis and design. New Delhi: Wiley Eastern Limited, 1985.
2. Holland ME. An experimental rainfall–runoff facility. In: Hydrology Papers. Colorado: Colorado State University, 1967.
3. Markovic RD. Probability functions of best fit to distributions of annual precipitations and runoff. In: Hydrology Papers. Fort Collins, Colorado: Colorado State University, 1976.
4. Pearson K. Table of incomplete gamma function. Cambridge: The University Press, 1957.
5. Zar JH. Biostatistical analysis. Englewood Cliffs, NJ 07632: Prentice Hall, Inc., 1984.
6. Gordon ND, McMahon TA, Finlayson BL. Stream hydrology: an introduction for ecologists. England: John Wiley and Sons Ltd, 1992.
7. KPCL. Draft policy paper on implementation of power projects by KPCL and private sector. Bangalore, India: Karnataka Power Corporation Ltd, 1993.
8. Subramanian DK. An optimal energy and water model for design and analysis of water resources of a river with constraints on energy and ecology. Technical Report No. 8. Bangalore, India: Centre for Ecological Sciences, Indian Institute of Science, 1985.
9. Maass A, Hufschmidt M, Dorfman R, Thomas HA, Marglin SA, Fair GM. Design of water resources systems––new techniques for relating economic objectives, engineering analysis and government planning. Cambridge, Mass.: Harvard University Press, 1962.
10.
Ramachandra TV. Bio energy potential and demand in Uttara Kannada district,
Karnataka. Special Issue on Bio Energy, IREDA News (India), 1996. ![]()
Table 10. Systems based on power and head: mini, micro and small hydro power plants
(8K)
*Corresponding author. Tel: +91-080-3340985; fax: +91-080-3315428; e-mail: cestvr@ces.iisc.ac.in
|
| ||||||||||||||||||||||||||||||||||
Volume 7, Issue 3 , March 1999 , Pages 195-211 | ||||||||||||||||||||||||||||||||||
| 11 of 30 |
|
Send feedback to ScienceDirect |